Dispersion in rectangular networks. Imagine that a pollutant is released accidentally in the centre of a city with a rectangular grid plan (such as Manhattan) on a windy day. How does this pollutant spread across the city? Similar questions arise in numerous other contexts -- how do chemical spread across the blood system, in porous media, in microfluidic channel devices, etc. We addressed these using the theory of large deviations, a sophisticated theory that finds here a remarkably simple application, leading to explicit results for the shape of patch of pollutant (Tzella and Vanneste 2016 and Physics Buzz).

Chemical front propagation in flows. In a wide variety of environmental systems such as the ocean and atmosphere and engineering applications, chemical or biological reactions propagate in the form of localized, strongly inhomogeneous structures associated with reactive fronts. These are usually established as a result of the interaction between molecular diffusion and local growth and saturation but their propagation can be greatly facilitated by advection which typically increases the effective area of the reaction. We investigated the influence of steady spatially periodic cellular flows on the propagation of chemical fronts arising in Fisher-Kolmogorov-Petrovskii-Piskunov type models. We used a WKB approach to provide a description of the front speed in the limit of small molecular diffusion and fast reactions (Tzella and Vanneste 2014). For slower reactions, the derivation of the front speed is obtained using matched-asymptotics analysis (Tzella and Vanneste 2015).

A popular alternative model of a chemical front is the G equation model. This was developed to provide a heuristic approximation to the FKPP front. A quantitative comparison between the two models is often challenging. We introduce a variational formulation that expresses the two front speeds in terms of periodic trajectories minimizing the time of travel across the period of the flow, under a constraint that differs between the two models (Tzella and Vanneste 2019). . This formulation makes it plain that the FKPP front speed is greater than or equal to the G equation front speed. We study the two front speeds for a class of cellular vortex flows and show that the differences between the two front speeds are modest for a broad range of parameters. However, large differences appear when a strong mean flow opposes front propagation; in particular, we identify a range of parameters for which FKPP fronts can propagate against the flow while G fronts cannot.

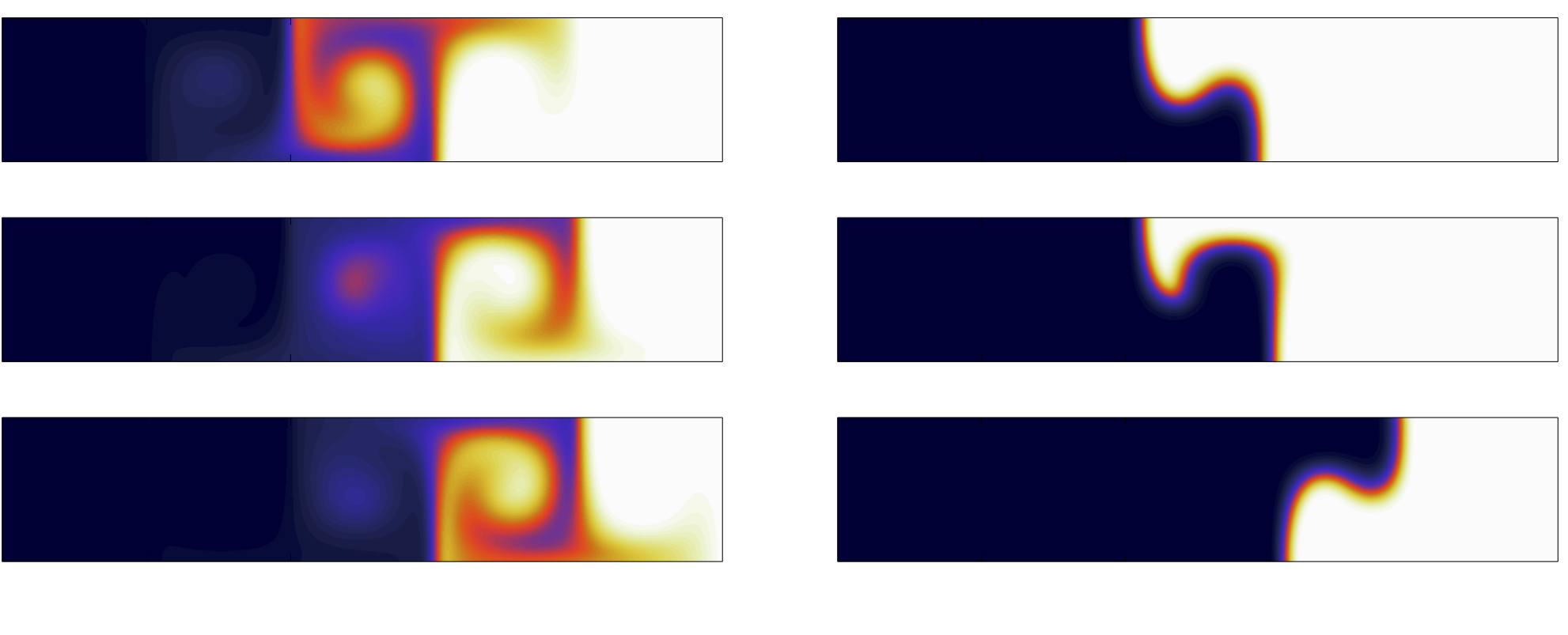
Spatial structure of chaotically mixed scalars. Motivated by the spatial heterogeneity observed in nutrient, phytoplankton and zooplankton distributions in the ocean at meso and sub-meso scales, we examined a class of biological models that, via a large-scale source, couple nutrients and plankton to a chaotic-advection flow. The particular emphasis has been on understanding the impact of the reactions and the intermittent nature of the flow on the corresponding filamental structures. The inclusion of a delay time in the reactions gives rise to a new scaling regime whose appearance depends on the magnitude of the delay time and the flow Lyapunov exponent (Tzella and Haynes 2007 Tzella and Haynes 2009). Another result emphasizes the dependence of the field's scaling exponents on the flow stretching statistics (Tzella and Haynes 2010).

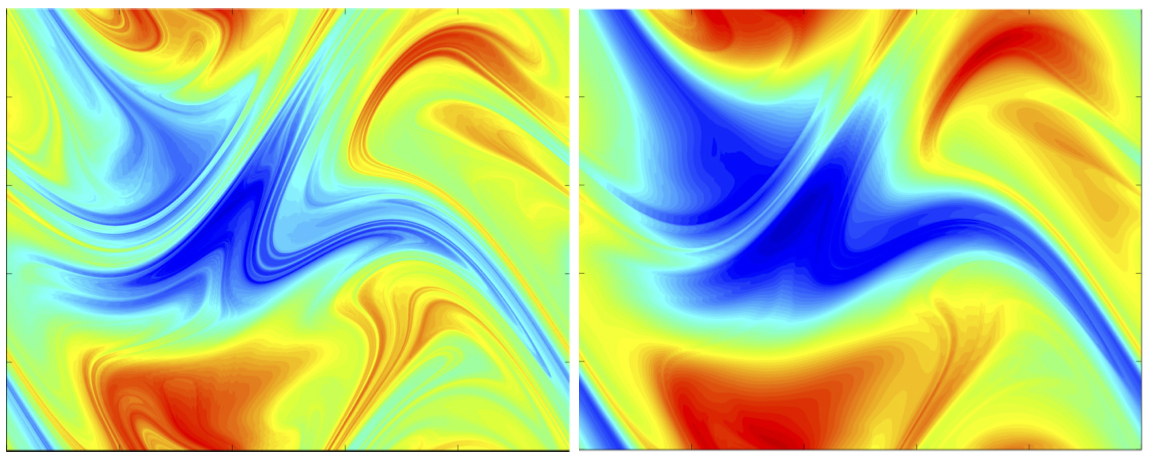
Mixing efficiency. There has lately been a lot of interest in quantifying the mixing efficiency of a continuously replenished scalar field. A set of bounds have been derived for the variance of the scalar and its gradient. Motivated by the apparent lack of control of the stirring process on these bounds, we focused on the characteristic lengthscale at which the variance is dissipated and derived a set of lower bounds for its value. For strongly stirring flows (high Péclet number), these lower bounds imply a number of regimes, one of which corresponds to the Batchelor regime. The transition between these regimes is controlled by the ratio of the characteristic lengthscale of the source and velocity field (Alexakis and Tzella 2011).

Transport within the Tropical Tropopause Layer (TTL). This is a key region now recognized to control most transport between the troposphere and the stratosphere. The efficiency of transport across the TTL depends on the continuous interaction between the large-scale advection and the small-scale intermittent convection that reaches the Level of Zero radiative Heating (LZH). Their combined effect can generate a large dispersion in the vertical transport times, particularly within the region encompassing the LZH, resulting in broad time distributions (Tzella and Legras 2011). This has implications for the amount of halogenated Very Short-Lived Substances (VSLS) that enter the stratosphere.