The Hilbert curve is one of a number of "space-filling curves", where a single curve (normally regarded as a one dimensional object) "fills" a higher dimensional space. In this case the space filled is the two dimensional area inside a square. (So the word "space" as in "space-filling" is taken in an abstract sense.)
Space filling curves can be defined for other applications too. For example it would be possible to define a curve that fills the interior of a cube. Points on the curve can be given by a single number, in other words using one degree of freedom. What this shows is that the idea of number of "degrees of freedom" is not really enough to define the traditional idea of dimension. In other words, all of these ideas of dimension are different abstractions of that familiar one. There does not appear to be any one single "good" concept of dimension, and one should take what is appropriate for the problem in hand.
Of course what one loses by switching from two degrees of freedom (for the interior of a square) to one degree of freedom (for the position on a curve) is simplicity. The Hilbert curve and many like it are very very complicated.
Not surprisingly perhaps, the Hilbert curve, since it fills a two dimensional space with a single curve, has fractional dimension of two.
The curve is obtained by starting with a simple path through the interior of the square,

The square is then divided into four smaller squares. For each smaller square, the existing line is "refined" in one of two ways. For a straight line, we use
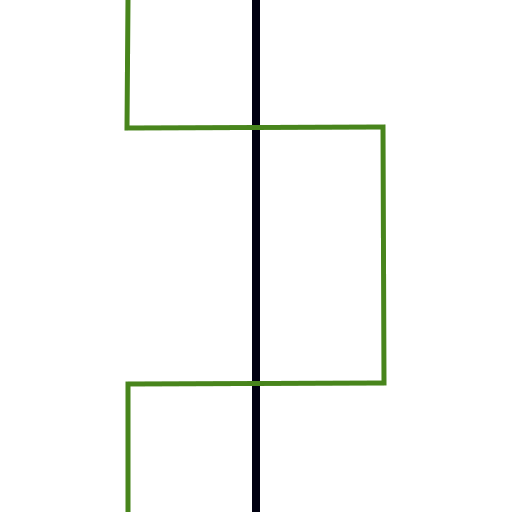
where black shows the original and the green is the refinement. For a corner we use
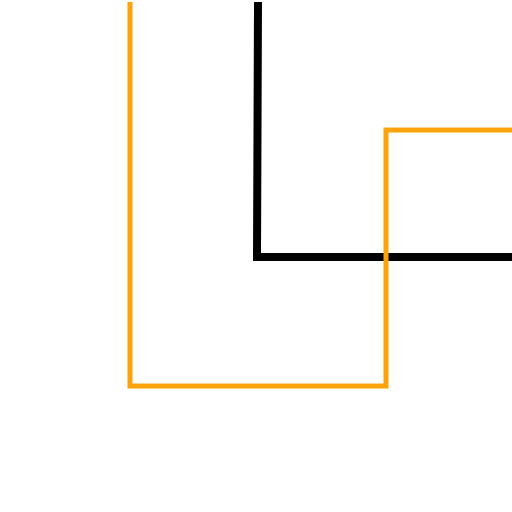
where the black is the original and yellow is the refinement. In many cases we will need some reflection or rotation of these patterns.
Doing this in all four of the smaller squares gives the next refinement of the Hilbert curve. The full square is then subdivided again and each section is refined again by the same rule. The following diagram shows the first refinement (black), second refinement (red) and third refinement (blue).
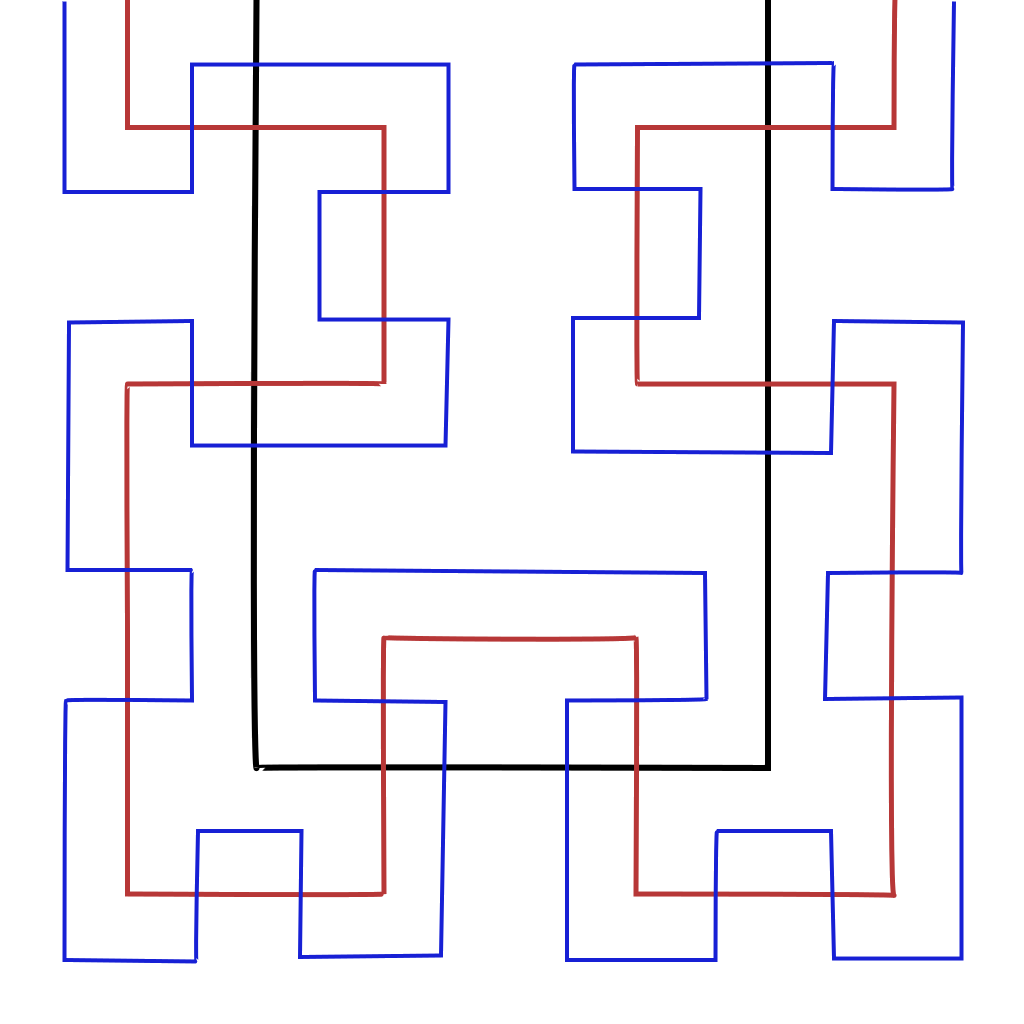
The final Hilbert curve is the limit of all these infinitely many iterations.
To work out the length of the Hilbert curve, suppose the original square has sides one unit. Then the first iteration has length two units. Each refinement doubles the length of the curve, and this doubling happens infinitely many times. So the total curve has infinite length! (Actually you might have expected that. It's a consequence of the fact that the fractional dimension is more than one. You will find the total length of the Koch snowflake curve is also infinite in the same sort of way.)
To work out the dimension of the Hilbert curve, look at the refinements of a path of length 1 in some square of side 1 and argue in rough terms as follows. (Note that a rigorous treatment of "fractional dimension" and its calculation in this case is beyond the scope of these notes, but the following gives the idea.) The length of the refinement is twice that of the original and this applies to both styles of refinement, but length is not quite this same as amount of stuff and the amount of stuff goes up by a factor of four. To see this note that, whereas one large circle of diameter one would have been sufficient to cover the whole of the original path, four circles of diameter a half are required to cover the new refined path. This shows that the "amount of stuff" in the final limiting case of the Hilbert curve increases by a factor of four as the linear dimension doubles. Since this means the Hilbert curve has fractional dimension . This again should be no surprise: it's a consequence of the fact that the Hilbert curve exactly fills the interior of the square.