Home
Curriculum Vitae Publications Ph.D.
Thesis
GEOMETRIC ASPECTS OF MINTY-BROWDER
MONOTONICITY
S. Z. Németh
Ph.D. thesis
Summary
Our dissertation presents some geometrical results concerning the Minty-Browder
monotonicity. In the first chapter different computational methods are
presented for determining the domains of monotonicity of an operator 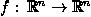 . Most of them are
connected to a new notion introduced by us the scalar derivative. In the
2-dimensional case the connection of the scalar derivative with the complex
derivative and Kasner circle is outlined.
. Most of them are
connected to a new notion introduced by us the scalar derivative. In the
2-dimensional case the connection of the scalar derivative with the complex
derivative and Kasner circle is outlined.
In the second chapter the notion of Minty-Browder monotonicity is extended to
Riemannian manifolds, introducing the monotone vector fields. The monotone
vector fields of gradient type were analyzed by C. Udriste and T. Rapcsák in
[34], [35] and [31]. However the nongradient case was not considered yet. We
deal mostly with this general case.
Connections with first variations of the length of a geodesic, closed
geodesics, one parameter expansive transformation groups, integral
submanifolds, auto-parallel submanifolds, the Lie derivative, conformal vector
fields, projection maps, nonexpansive maps, singularities of vector fields are
exhibited. Throughout the dissertation many examples are given, and different
computation methods are presented for determinining the domains of monotonicity
of a vector field. Most of them are connected with a new notion introduced by
us the geodesic scalar derivative. We generalized the notion of monotonicity,
introducing the pseudomonotone, strictly pseudomonotone and quasimonotone
vector fields. Connections with the corresponding types of convexities are
presented.
Introduction
The Minty-Browder monotonicity notion was an important achievement of nonlinear
analysis. It throws a new light on many known results and becomes a good
instrument in various application oriented new investigations.
Convex functionals in Hilbert spaces have as gradients monotone operators. This
result was extended to Riemannian manifolds by C. Udriste [34], [35]. He proved
that the gradient of a (geodesic) convex functional [31] on a Riemannian
manifold is monotone. T. Rapcsák [31] gives a more explicit form of this
result. Hovewer, there are nongradient type monotone vector fields which (as
far as we know) has not been studied yet.
Recent developments of convex optimization problems on Riemannian manifolds
[31] focus the attention to nongradient type monotone vector fields, since in
the Hilbert case in the analysis and solution of complementary problems,
variational inequalities, and evolution equations it is commonly assumed that
the defining map is monotone (and not necessarily of gradient type).
The main purpose of our thesis is to present global results on the geometrical
aspects of the Minty-Browder monotonicity. We consider that this notion has a
strong geometrical meaning, which has not been analysed yet.
The thesis is structured on chapters, sections and subsections. The first
chapter is devoted to the euclidean case. It contains three sections. The first
two deals with first order characterizations of monotone maps through the scalar
derivative, a new notion introduced by us. In the two dimensional case the
connection of scalar derivatives with the complex derivative and the Kasner
circle is also encountered.
The third section analyses the connection of scalar derivative with conformity.
It is proved that globally scalar differentiability of a map (which can be
identified with a vector field) implies the conformity of the one parameter
transformation group generated by this map (vector field). Locally, the
connection is given using the conformal derivative, a new notion introduced by
us. In this section the well-known connection between monotone operators and
nonexpansive semigroups [40] is also presented, from a more geometrical point
of view.
The second chapter is devoted to the Riemannian case. It contains six sections.
In the first section the notion of geodesic monotone vector fields is
introduced [35], which generalize the monotone operators. First order
characterization of geodesic monotone vector fields are given, using the
geodesic scalar derivatives, a new notion introduced by us. Different
computational formulae are presented for this derivative. The constant
curvature case is analysed separately, since it has important peculiarities. We
present the connection of geodesic monotone vector fields with the first
variation of lengths of geodesics and the existence of closed geodesics. For
Hadamard manifolds (complete, simply connected Riemannian manifolds of
nonpositive sectional curvature) a class of geodesic monotone vector fields is
given which generalize the position vector fields [26]. It is proved that there
are monotone vector fields on Hadamard manifolds, which are not gradient
fields.
In the second section we analyse the connection of geodesic monotone vector
fields with one parameter expansive transformation groups. We introduce the
Killing monotone vector fields, which are the vector fields generated by such
transformation groups. We proved that the notion of Killing monotone vector
fields and geodesic monotone vector fields coincide. For brevity's sake they
are called monotone vector fields. These results are generalizations of the
results of section 1.3.2. We also analyse the connection of the Lie derivative
with monotonicity and (geodesic) scalar derivatives. It is proved that a vector
field is conformal if and only if it is (geodesic) scalar differentiable,
generalizing the corresponding result of section 1.3.1.
The third and fourth section deals with complementary vector fields of maps on
Hadamard manifolds. We define the notion of complementary vector fields
and 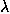 -complementary vector
fields of maps on Hadamard manifolds. It is proved that for
-complementary vector
fields of maps on Hadamard manifolds. It is proved that for 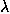 increasing the
increasing the 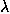 -complementary vector fields of projection maps to
closed (geodesic) convex sets [31] are monotone. It is also proved that the
complementary vector fields of nonexpansive maps are monotone. As a particular
case composition of projection maps to closed convex sets are considered. These
results are generalizations of some results of [38].
-complementary vector fields of projection maps to
closed (geodesic) convex sets [31] are monotone. It is also proved that the
complementary vector fields of nonexpansive maps are monotone. As a particular
case composition of projection maps to closed convex sets are considered. These
results are generalizations of some results of [38].
In the fifth section different types of generalized monotone vector fields are
introduced. It is showed that for gradient fields, these generalized
monotonicity properties correspond to generalized convexity properties of the
underlying functions. These results extend some results of [11].
In the sixth section we prove that the zeros of a monotone vector field,
defined in a convex open subset of an Hadamard manifold, form a convex set.
Home
Curriculum Vitae Publications Ph.D.
Thesis