





The proof that S refines R is by looking at cases. Let x,y be in A with xRy. Suppose x,y are both in A'. Then xR'y so xS'y so xSy. If x=a and y is in A' then aRy so y is in L so x0S'y by the fact so aSy by the definition. If y=a and x is in A' then xRa so x is in U so xS'x0 by the definition of x0, so xSa by the definition of S. Finally aSa by definition of S, covering the case when x=y=a.
The proof that S is a linear order is similar. It is reflexive since aSa by definition, and xSx for all x in A' since S' is reflexive.
It is transitive since if xSy and ySz we can show xSz by looking at all the cases (whether or not x,y, or z is equal to a). We may suppose that x,y,z are all different (for otherwise transitivity is easy). If none of x,y,z equals a then xS'y and yS'z so xS'z so xSz by transitivity of S' and the definition of S. If x=a and aSy and ySz then x0S'y and yS'z and y is not equal to x0, hence x0S'z by transitivity and z is not equal to x0 by antisymmetry, so aSz. If y=a and xSa and aSz then xS'x0 and x0S'z and z is not equal to x0, hence xS'z so xSz. If z=a and xSy and ySa then xS'y and yS'x0, hence xS'x0 so xSa.
It is antisymmetric since S' is antisymmetric (this covers the cases when xSy and ySx with neither x,y equal to a) and if x=a, y not equal to a, aSy and ySa then x0S'y , y not equal to x0, and yS'x0 contradicting the antisymmetry of S'.
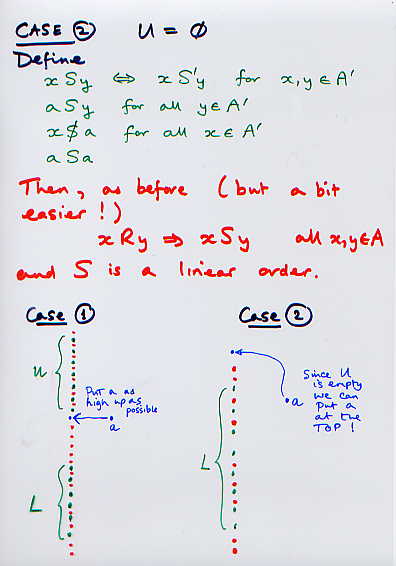
The proof in case 2 that S is a linear order that refines R is similar to the one for case 1, except it is easier since there are fewer cases to consider. This is left as a (moderately awkward) exercise for energetic students!
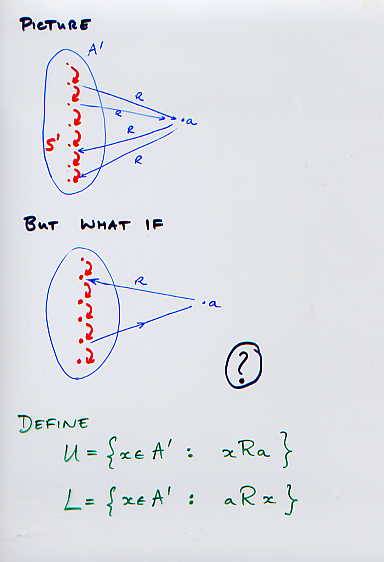
The two pictures in the last slide show what the effects of the definitions in cases 1 and 2 are to the order. In both cases we are putting a as "high as possible".