Entwurf neuer Materialien

        Prof. Dr. Jochem Zowe

Eines der grundlegenden Strukturprobleme lautet wie folgt: Man finde für eine gegebene Menge von Randbedingungen und Kräften die leichteste Struktur, die die gegebenen Kräfte tragen kann.

Die Strukturoptimierung wurde ursprünglich mittels Variation von Sizingvariablen (z.B. Dicke eines Stabes in einem Stabwerk) und Formvariablen (z. B. Splines, die den Rand eines Körpers definieren) durchgeführt. Mit dem Aufkommen von Verbundmaterialien und anderen neuen Materialien (advanced materials) lag es auf der Hand die Auswahl des Materials selbst in der Optimierung zu berücksichtigen. In den letzten Jahren machte die wachsende Entwicklung von mathematischen Methoden ein starkes Interesse an diesem ,,verallgemeinerten'' Problem des optimalen Designs deutlich. Diese Methoden, die üblicherweise als Topologie- bzw. Materialoptimierungsmethoden bezeichnet werden, haben zum Ziel sowohl die Gestalt und die Topologie, als auch die Materialeigenschaften elastischer Körper zu optimieren. Die Entwicklung dieser Methoden hat ihren Ursprung in den achtziger Jahren, als eine Reihe von theoretischen Abhandlungen über Relaxierungsverfahren (Allaire-Kohn) bzw. Homogenisierungsverfahren (Bendsøe) mit möglichen Anwendungen auf das Problem des optimalen Designs erschienen. Das Interesse der Ingenieure wurde erst durch die Pionierarbeit von Bendsøe und Kikuchi geweckt, die ein auf den Homogenisierungsmethoden basierendes numerisches Verfahren einführten und damit den praktischen Nutzen der zuvor entwickelten theoretischen Methoden nachwiesen. Seitdem wurden zahlreiche ähnliche Zugänge und Techniken entwickelt; ein Überblick kann z.B.bei Allaire-Kohn oder Bendsøe gefunden werden.

Trotz dieses vielversprechenden Auftaktes folgte bald ein Rückschlag. Obige Verfahren führen gewöhnlich zu (Approximationen von) optimalen, die sich von Punkt zu Punkt unterscheiden können und daher sehr schwer herstellbar sind. Die Teile des Körpers, in denen das Material ,,verschwindet'' werden als Löcher interpretiert. Die Interpretation im restlichen Körper ist jedoch häufig unklar. Die erzielten Ergebnisse enthalten typischerweise Informationen über eine Art von Dichte des Materials in jedem Punkt. Dies ist zum Beispiel das Verhältnis von Material und ,,Nicht-Material'' in einer mikroskopischen Zelle, d. h. eine Zahl zwischen Null und Eins. Es wird jedoch noch mehr an Information gewonnen, so zum Beispiel die Anordnung des Materials in einer Mikrozelle, ob es etwa eine (Mikro-)faser darstellt und der Anordnungswinkel. Diese zusätzlichen Informationen werden oft vernachlässigt. Die meisten in letzter Zeit erschienenen Ansätze neigen dazu, nur die Dichte im Null-Eins- (bzw. Material-Nichtmaterial-) Sinne zu interpretieren. Daher versuchen solche Methoden, entweder bereits im Modell oder durch gezielte Nachbearbeitung die Bereiche, in denen Dichtewerte zwischen Null und Eins angenommen werden, zu minimieren. Ein solches Vorgehen kann jedoch nicht im Sinne der Materialoptimierung sein, denn man weiß: das verallgemeinerte Problem des optimalen Designs besitzt keine Null-Eins Lösung.

Um die Materialoptmierungseigenschaften voll auszuschöpfen ist es daher wichtig, die gesamte Information, die aus den Ergebnissen gewonnen werden kann, auszunutzen und konsequenterweise den Schritt von herkömmlichen Materialien zu neuen Materialien zu gehen.

Wir stellen hiermit eine Sammlung von Werkzeugen des konzeptionellen Strukturdesigns, namens MOPED vor. Das zugrundeliegende Modell ist das von Bendsøe et al. eingeführte und von Kocvara et al. und Zowe et al.  fortgeführte free  material optimization Problem. Unser Ziel ist es, nicht nur die Verteilung des Materials, sondern auch die Materialeigenschaften selbst zu optimieren. Wir suchen daher nach der bestmöglichen, elastischen, kontinuierlichen Struktur. Für diese Methode stehen mächtige Optimierungswerkzeuge und numerische Verfahren zur Verfügung, die uns erlauben mit komplexen Ausgangsdesigns und sehr feinen Netzen finiter Elemente zu arbeiten. Daher sind wir in der Lage auch in ,,schwierigen'' Bereichen und für komplexe Geometrien sehr genaue Ergebnisse zu erzielen.

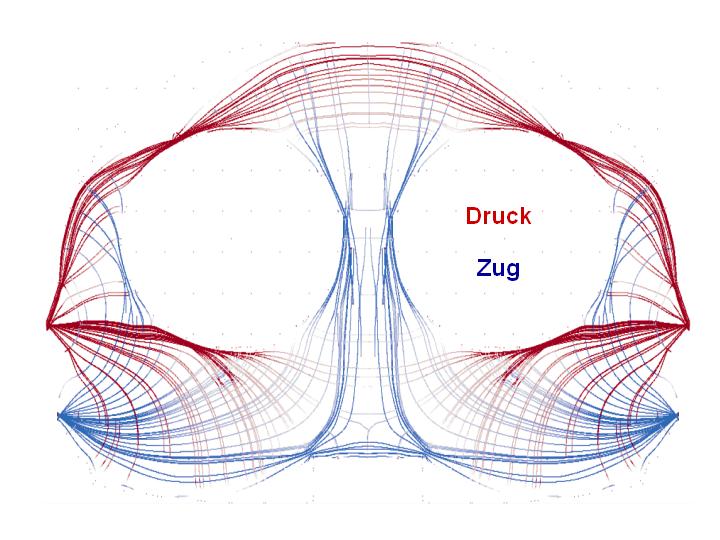
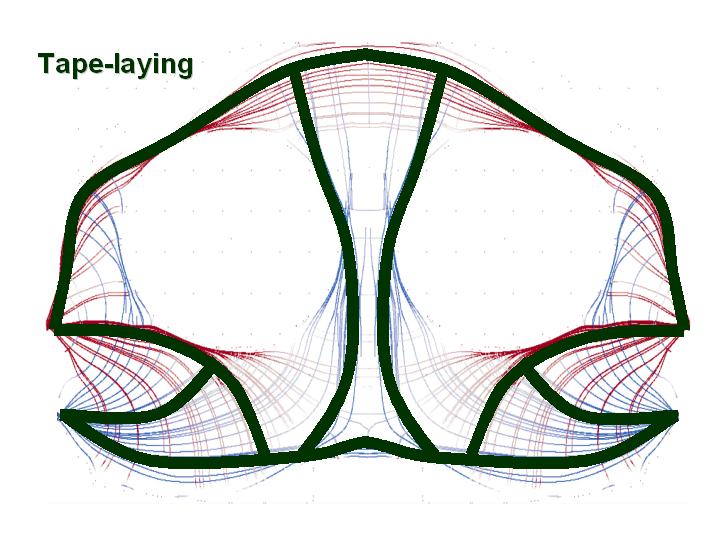
Statt uns auf die Interpretation im Null-Eins-Sinne zu beschränken, wollen wir die volle in den Ergebnissen enthaltene Information verwenden, um neue herstellbare Materialien zu entwerfen. Dies hängt offensichtlich vom Typ des Materials und den Produktionstechniken ab. Die Kompositmaterialien selbst zeigen uns den Weg zur Umsetzung der berechneten Ergebnisse. Wir betrachten eine bestimmte Menge von Kompositmaterialien, die durch die sogenannte ,,tape-laying'' Technik hergestellt werden können. In der Phase der Nachbearbeitung zeichnen wir Kurven, die angeben in welcher Weise die Bahnen (tapes) im Kompositmaterial abgelegt werden; aus diesen Kurven geht darüberhinaus die Dicke der Bahnen hervor.

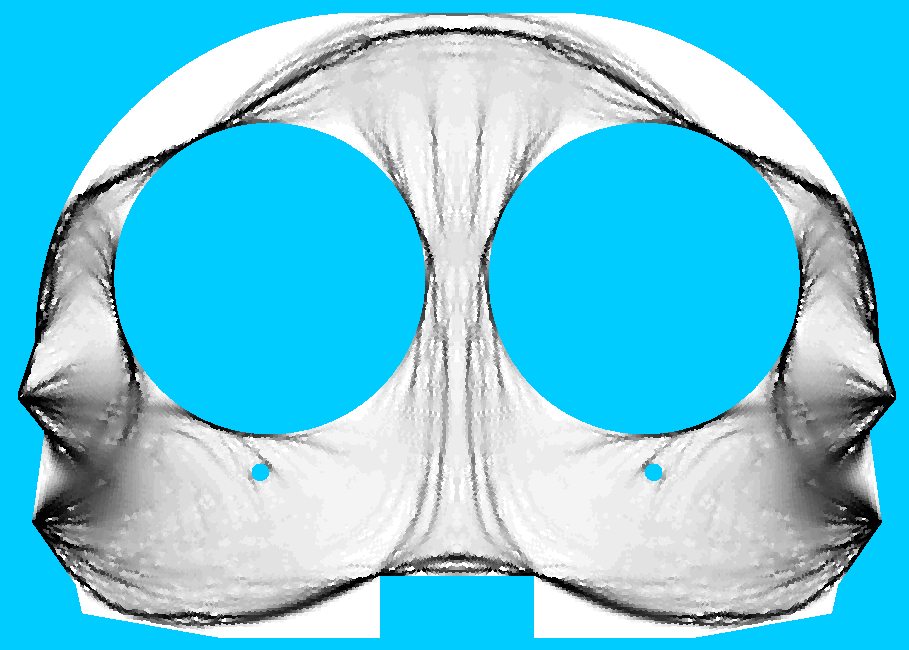
MOPED wurde im Rahmen des BMBF Projektes Optimization of Discrete and Continuous Mechanical Structures in Zusammenarbeit mit unserem Industriepartner DaimlerChrysler Aerospace AG aus München entwickelt. Zur Illustration folgt unten ein typisches Beispiel, das für unseren Partner berechnet wurde. Das Ziel war, einen Querschnitt durch den Rumpf eines Flugzeuges zu entwerfen, das sehr großen Kräften widerstehen muß, die in extremen Flugsituationen von den Flügeln auf den Rumpf übertragen werden. Das folgende Bild zeigt das Anfangslayout.

Lebenslauf

Literaturverzeichnis

A. Ben-Tal, M. Kocvara, A. Nemirovski, and J. Zowe. Free material design via semidefinite programming. The multi-load case with contact conditions. SIAM J. Optimization, 9(4): 813-832, 1999.

M. P. Bendsøe. Optimization of Structural Topology, Shape and Material. Springer-Verlag, Heidelberg, 1995.

M. P. Bendsøe and N. Kikuchi. Generating optimal topologies in structural design using a homogenization method. Comp. Meth. Appl. Mechs. Engrg., 71:197-224, 1988.

M. P. Bendsøe, J. M. Guades, R. B. Haber, P. Pedersen, and J. E. Taylor. An analytical model to predict optimal material properties in the context of optimal structural design. J. Applied Mechanics, 61:930-937, 1994.

M. Kocvara, M. Stingl, and R. Werner. MOPED User's Guide. Version 1.02. Research Report 262, Institute of Applied Mathematics, University of Erlangen, 2000.

M. Kocvara, M. Zibulevsky, and J. Zowe. Mechanical design problems with unilateral contact. M2AN Mathematical Modelling and Numerical Analysis, 32:255-282, 1998.

J. Zowe, M. Kocvara, and M. Bendsøe. Free material optimization via mathematical programming. Mathematical Programming, Series B, 79:445-466, 1997.

WWW-links

Technische Universität Denmark: http://Feodora.fam.dtu.dk/Theory1/index.html

Universität Stuttgart: http://www.uni-stuttgart.de/ibs/res_5.html