Using subsequences to prove convergence

Exercise.

A student is applying for a job and folds the covering letter (which is written on a sheet of paper of length 1) into thirds to put it in the envelope, using the following method:

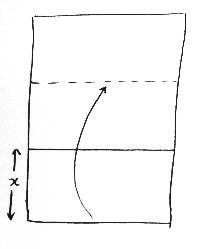
image of fold1 image of fold2

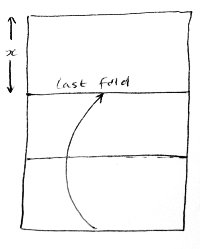
First a fold is made along a horizontal line distance from the bottom of the paper (where 0 12 and is chosen at random). The paper is unfolded and turned upside down.
Next, the paper is folded so that the bottom edge lies exactly on the last fold just made. The paper is unfolded and turned upside down once again.
The process in the last paragraph is repeated.

(a) Explain why, if the distance from the bottom of the first fold is ₁₌, the distance from the bottom of the +1st fold is given by _+1=12(1-₎ .

(b) Prove that _+2=14(1+₎ for all , and use this to show that

2+1 =13+ 4 -13 4

and

2+2 =13+14 1-2 -13 4

for all 1 . (Use induction on .)

(d) Which standard theorem in these notes allows you to conclude from (c) that ₁₃ as ?

If you are still struggling with the idea of the definition of convergence think of it as saying whatever the size of the envelope, as long as it is a small amount more than 13, then some number of steps of this process is guaranteed to get the paper folded in a way to get it in the envelope. Of course, your job prospects may also depend on other things too, such as a nice crisp and uncreased covering letter... ;)

Exercise.

Let ₀₌₁ and ₊₁₌₁₊₁ . By considering the subsequences ₂ and ₂₊₁ show that ₁₊₅₂.

Using subsequences to prove convergence - exercises