On the irreducible character degrees of symmetric groups and their multiplicities
October 4, 2024
We consider problems concerning the largest degrees of irreducible characters of symmetric groups, and the multiplicities of character degrees of symmetric groups. Using evidence from computer experiments, we posit several new conjectures or extensions of previous conjectures, and prove a number of results. One of these is that, if \(n\geq 21\), then there are at least eight irreducible characters of \(S_n\), all of which have the same degree, and which have irreducible restriction to \(A_n\). We explore similar questions about unipotent degrees of \(\GL _n(q)\). We also make some remarks about how the experiments here shed light on posited algorithms for finding the largest irreducible character degree of \(S_n\).
Contents
1 Introduction
The multisets of degrees of the irreducible characters of the symmetric groups \(S_n\) have been studied for over a century. Over the last 50 years or so there has been work on two particular aspects of this: the largest degrees of irreducible characters, and the multiplicities of irreducible character degrees. Here we will propose a few new conjectures and avenues of research, on the basis of experiments with symmetric groups of degree up to around 120, along with some new results in this area.
We start with multiplicities. If \(G\) is a finite group, write \(m(G)\) for the maximal multiplicity of an irreducible character degree of \(G\), and write \(m(n)=m(S_n)\). In [3] it was proved that \(m(n)\to \infty \) as \(n\to \infty \), and together with [17] this proves that \(m(G)\to \infty \) as \(|G|\to \infty \). A natural question is to ask for the growth rate of \(m(G)\) in general, and \(m(n)\) in particular. A lower bound for the growth of \(m(n)\), approximately \(n^{1/7}\), was proved in [4, Theorem E], but this is far from optimal, and is a remnant of the methods of [3]. The theorem we prove here is the following, which has been used in [15] to find all finite groups \(G\) for which \(m(G)=2\). This result is a slight specialization of Theorem 3.2 below.
-
Theorem 1.1. If \(n\geq 11\) then \(m(n)\geq 4\). If \(n\geq 17\) then \(m(n)\geq 6\). If \(n\geq 21\) then \(m(n)\geq 8\). In each of these cases, it is possible to choose four, six and eight irreducible characters respectively that are of the same degree and also have irreducible restriction to \(A_n\).
For small values of \(n\) it is possible to prove this theorem by simply finding a number of characters of the same degree. Above this we need a blend of techniques from [3] and computer methods to complete the proof. Using a computer, in Table 4.1 we give the value of \(m(n)\) for \(n\leq 115\). For \(n\geq 206\) one can prove the result by explicitly giving eight characters with the same degree. Between these bounds one needs to prove the result using a computer; this yields explicit characters but there is no generic nature to them, unlike the situation for \(n\geq 206\).
Since the degrees of the unipotent characters of the general linear groups are related to those of symmetric groups, it is reasonable to suspect that one might be able to say something about multiplicities of character degrees for general linear groups. As we see in Section 2.2, the degrees of the characters associated to a partition and its conjugate, while equal for \(S_n\), are generally not for \(\GL _n(q)\), so it is not even clear that there are two unipotent characters with the same degree for \(\GL _n(q)\). To the author’s knowledge there is no established theory about this in the literature, so this paper starts the investigation of this subject, with the following contribution.
-
Proposition 3.5. If \(\lambda \) is a partition of \(n\), let \(\chi _\lambda \) denote the corresponding unipotent character of \(\GL _n(q)\). If \(n=15,16,19,20,21,22\) or \(n\geq 24\) then there is a partition \(\lambda \) such that the generic degrees of \(\lambda \) and the conjugate partition \(\lambda '\) are the same. Otherwise there is no such partition.
As \(n\) increases the number of partitions \(\lambda \) with this property seems to grow quickly (see Table 4.2), but the author can envisage no obvious proof of this.
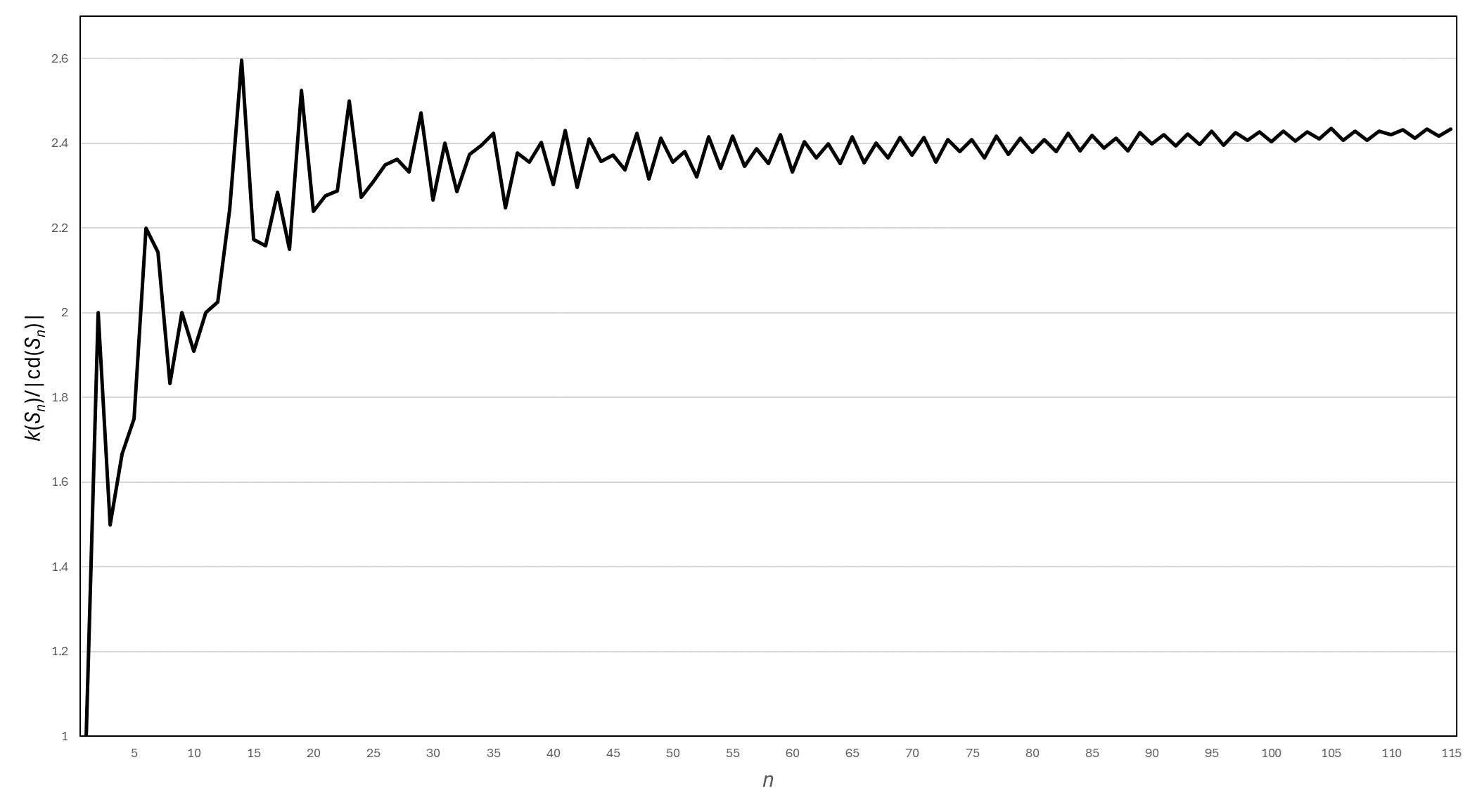
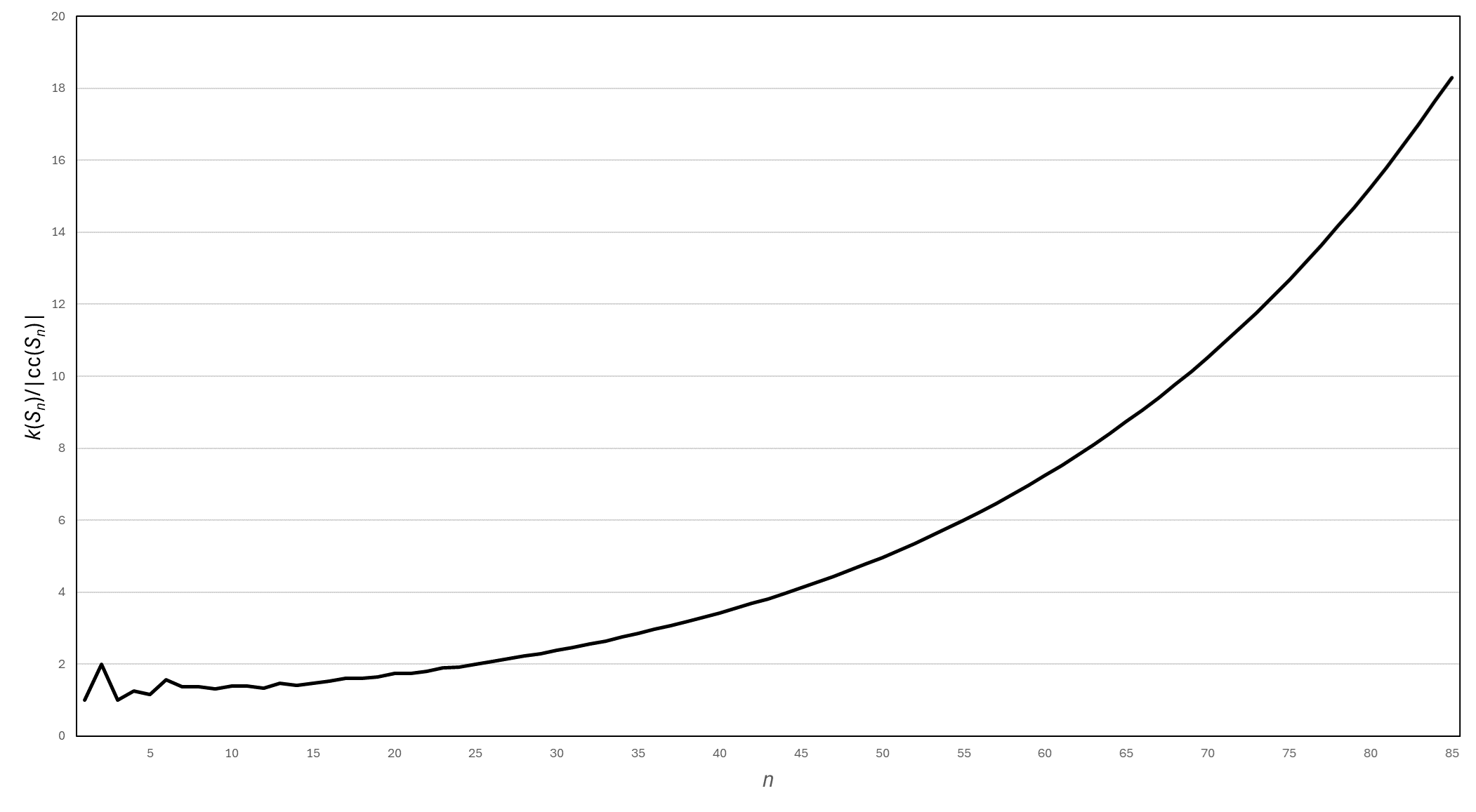
Connected to the maximal multiplicity of a character degree we have the average multiplicity of a character degree. Write \(k(G)\) for the number of conjugacy classes of a finite group \(G\), or equivalently the number of irreducible characters of \(G\). Let \(\cd (G)\) denote the set of irreducible character degrees of \(G\), and \(\cc (G)\) denote the set of conjugacy class sizes of \(G\). The average character degree multiplicity is \(k(G)/|\cd (G)|\), and the average conjugacy class size multiplicity is \(k(G)/|\cc (G)|\). We compute both of these for symmetric groups; the former is calculated up to \(S_{115}\), with a pattern emerging (see Figure 3.1) but the asymptotics remaining unclear at this stage. For conjugacy classes, only data up to \(S_{85}\) was necessary for a convincing conjecture to emerge (Figure 3.2). The following two conjectures are considered in more detail in Section 3, and the concepts have been considered before, for example in [10, 17].
We also consider the largest degrees of \(S_n\). Let \(b_1(n)\) denote the largest character degree of \(S_n\), \(b_2(n)\) the second largest, \(b_3(n)\) the third largest and so on. In [8], it was proved that, for \(n\geq 7\), we have that
\[ \sum _{\substack {\chi \in \Irr (S_n)\\\chi (1)<b_1(n)}} \chi (1)^2>2b_1(n)^2.\]
Experimental data about the submaximal degrees \(b_2(n)\), \(b_3(n)\), and so on, collated in Section 4, gives a solid basis for believing the following conjecture.
-
Conjecture 4.1. Let \(n\) be an integer with \(n\geq 5\), \(n\neq 6,7\).
-
(i) If \(n\neq 11\) then \(b_1(n)^2\leq b_2(n)^2+b_3(n)^2\).
-
(ii) If \(n\neq 6,7,11,16,38\), and \(b_2(n)\) or \(b_3(n)\) is achieved by two or more irreducible characters of \(S_n\), then
\[ \sum _{\substack {\chi \in \Irr (S_n)\\\chi (1)\in \{b_2(n),b_3(n)\}}}\chi (1)^2>2b_1(n)^2.\]
-
(iii) If \(b_2(n)\) and \(b_3(n)\) are both achieved by a unique irreducible character of \(S_n\) then
\[ \sum _{\substack {\chi \in \Irr (S_n)\\\chi (1)\in \{b_2(n),b_3(n),b_4(n)\}}}\chi (1)^2>2b_1(n)^2.\]
-
(iv) If \(n\geq 62\) then \(2b_1(n)^2\leq b_2(n)^2+b_3(n)^2+b_4(n)^2\).
-
It appears as though the ratio \(b_2(n)/b_1(n)\) tends to \(1\) as \(n\) grows, so that there is no single large degree for symmetric groups, see Figure 4.1. We posit that, in fact, this is true for any fixed \(m\), so \(b_m(n)/b_1(n)\to 1\) as \(n\to \infty \).
At the end of Section 4 we also include some information about how far the partitions \(\lambda ^{(n)}\) witnessing \(b_1(n)\) stray from being self-conjugate. Contrary to what might be considered reasonable – that as \(n\) increases the partition becomes closer and closer to self-conjugate (mimicking the curve known to maximize the continuous version of the hook length formula found in [14, 21]) – it seems that the difference between \(\lambda ^{(n)}\) and a self-conjugate partition is unbounded as \(n\) grows. This has implications for any posited algorithms for guessing the largest-degree character that start by looking at self-conjugate partitions.
All the conjectures and results herein were based on calculations using Magma [1], and in particular the package symmetric, developed by the author. This package contains programs to compute all information described in this article, and most information is furthermore stored in databases in the package, for ease of access. The package, together with documentation on the included programs, is available on the author’s website, GitHub, and the arXiv page for this article.
I would like to thank Benjamin Sambale for noting an error in the formulation of Conjectures 3.3 and 3.4.
2 Preliminaries
Our notation is almost entirely standard.
2.1 Symmetric groups
Here we summarize the theory of the symmetric groups that we need, together with some terms and results from [3] that will be useful. A general introduction to the theory of representations of symmetric groups can be found in a number of places, for example [11, 12, 20].
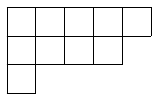
The irreducible representations/characters of the symmetric group \(S_n\) over a field of characteristic \(0\) are labelled by partitions \(\lambda \). The most important part of this for us is the hook formula. First, we note the pictorial description of partitions known as Young diagrams (also known as Ferrers diagrams). Ordering the parts of \(n\) in the partition \(\lambda =(\lambda _1,\dots ,\lambda _r)\) so that \(\lambda _i\geq \lambda _{i+1}\) for all \(i\) (for us, partitions satisfy \(\lambda _i>0\) for all parts), the Young diagram has \(\lambda _i\) boxes in row \(i\), aligned left. For example, the Young diagram for the partitions \((5,4,1)\) is below.
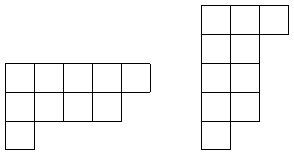
The conjugate partition is the partition obtained by reflecting the Young diagram in the diagonal line in the \(y=-x\) direction through the top-left box. For example, the conjugate partition of \((5,4,1)\) is \((3,2,2,2,1)\).
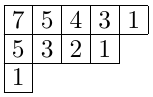
Given a box in the Young diagram of a partition \(\lambda \), the hook consists of the box itself, all boxes below it in \(\lambda \), and all boxes to the right of it. The length of the hook is the number of boxes in the hook. For example, the lengths of the hook in the boxes of \((5,4,1)\) are given below.
Notice that a partition and its conjugate have the same multiset of hook lengths.
If \(\chi _\lambda \) denotes the irreducible character of \(S_n\) labelled by \(\lambda \) then the degree of \(\chi _\lambda \) is
\[ \chi _\lambda (1)=\frac {n!}{\prod _{(i,j)\in \lambda } h_{i,j}},\]
where the product runs over all boxes \((i,j)\) in \(\lambda \) and \(h_{i,j}\) is the hook length at the box \((i,j)\). Let \(H(\lambda )\) denote the multiset of hook lengths of \(\lambda \).
At one point we will use the branching rule. If \(\lambda \) is a partition of \(n\), then a removable node is a box in the Young diagram of \(\lambda \) that, upon removal, yields a Young diagram of a (smaller) partition. This is equivalent to the box having hook length \(1\). The opposite is an addable node: an addable node is a node that is not in the Young diagram of \(\lambda \) but, if it is added to \(\lambda \), the result is also the Young diagram of a partition.
The branching rule states that if \(\lambda \) is a partition of \(n\), then the restriction of \(\chi _\lambda \) to \(S_{n-1}\) is the sum of all irreducible characters \(\chi _\mu \) such that \(\mu \) is obtained from \(\lambda \) by removing a removable node. By Frobenius reciprocity, the induction of \(\chi _\lambda \) to \(S_{n+1}\) is the sum of \(\chi _\mu \) for \(\mu \) obtained from \(\lambda \) by adding an addable node.
We now recap some definitions and results from [3]. Let \(\Lambda \) be a set of partitions, all of the same integer \(n\). The set \(\Lambda \) is a cluster if all elements of \(\Lambda \) have the same hook lengths, i.e., \(H(\lambda )=H(\mu )\) for all \(\lambda ,\mu \in \Lambda \). Since there is both the cardinality of the cluster and the number that the elements of the cluster are partitions of, we will say that the size of the cluster is the size of the partitions in it, and the order of the cluster is the number of elements in the cluster. A cluster is periodic of period \(p\) if, for all \(n\geq 0\), adding \(n\) boxes to the first \(p\) rows of all partitions in \(\Lambda \) forms another cluster. For example, the cluster \(\{(5,2,2,2),(4,4,1,1,1)\}\) is periodic of period \(3\), because \(\{(n+5,n+2,n+2,2),(n+4,n+4,n+1,1,1)\}\) is also a cluster for all \(n\geq 0\). (This example comes from [9].) If \(n=0\) then the two partitions in the cluster are conjugate, but this is not the case for \(n\geq 1\), so together with their conjugates we find four partitions with the same hook lengths for all integers of the form \(3n+11\), \(n\geq 1\).
To prove that a cluster is periodic of period \(p\) we may use [3, Theorem 4.2], which asserts that a cluster is periodic if it satisfies two easy-to-check criteria. The first of these is that if one removes the first \(p\) parts of all partitions in the cluster, we obtain another cluster. The second is that the multisets \(\{(\lambda _i-\lambda _j)-(i-j)\mid 1\leq i<j\leq p\}\) are the same for all partitions \(\lambda \) in the cluster.
2.2 General linear groups
The complex character theory of the general linear groups \(\GL _n(q)\) uses many of the combinatorial concepts involved in symmetric groups such an hook lengths. One may find a description of some of this theory in [2].
We consider a subset of the ordinary characters, called unipotent characters. These are labelled by partitions of \(n\), and their degrees are polynomials in \(q\). If \(\lambda =(\lambda _1,\dots ,\lambda _r)\) is a partition of \(n\), define Lusztig’s \(a\)-function by
\[a(\lambda )=\sum _{i=1}^r (i-1)\lambda _i.\]
The degree of the character \(\chi _\lambda \) is
\[ \chi _\lambda (1)=q^{a(\lambda )}\frac {\prod _{i=1}^n (q^i-1)}{\prod _{h\in H(\lambda )} (q^h-1)}.\]
Thus \(\chi _\lambda (1)=\chi _\mu (1)\) (for all \(q\)) if and only if \(H(\lambda )=H(\mu )\) and \(a(\lambda )=a(\mu )\).
Generic degrees can be found using cyclotomic Hecke algebras, and in the best-case scenario there is a single unipotent character with that generic character degree. Coincidences between generic degrees of unipotent characters make it more difficult to understand the bijection between irreducible unipotent characters in a block of \(\GL _n(q)\) and the simple modules for the Brauer correspondent given by the cyclotomic Hecke algebra. This is an important part of various formulations of Broué’s conjecture for groups of Lie type, so this question has ‘real-world’ applications [5, 6].
3 Maximal and average multiplicities
3.1 Symmetric groups
Determining whether two partitions \(\lambda \) and \(\mu \) have the same product of hook lengths looks a difficult task, which is why in [3] the author worked with the tighter condition that the hook lengths are identical, not merely that their products were identical. This, of course, has the downside that one misses many pairs of partitions with the same product of hook lengths. In this section we look at both whether partitions have the same multiset of hook lengths and whether they have the same products of hook lengths. After this, we consider the situation for \(\GL _n(q)\).
First we see what we can prove about the case where the multiset of hook lengths must be the same, rather than their product.
-
-
(i) There is a cluster of order \(4\) and size \(n\) if and only if \(n\geq 22\) or \(n=14,17,19,20\).
-
(ii) There is a cluster of order \(8\) and size \(n\) if \(n\geq 206\). If \(n\leq 83\), the largest order of a cluster of size \(n\) is \(4\), whereas there is a cluster of order \(8\) and size \(84\).
-
-
Proof. We first consider clusters of order \(4\). In [9], Herman and Chung find two periodic clusters of order \(2\):
\[\{(n+6,n+3,n+3,2),(n+5,n+5,n+2,1,1)\},\qquad \{(n+8,n+4,n+3,3,1),(n+7,n+6,n+2,2,1,1)\}.\]
Together with their conjugates, this yields a cluster of size \(4\) for all \(3n+14\) and \(3n+19\) with \(n\geq 0\). In [3] another periodic cluster of period \(3\) was found:
\[ \{(n+10,n+4,n+4,4,2),(n+8,n+8,n+2,2,2,1,1)\}.\]
This yields a cluster of size \(4\) for all \(3n+24\) with \(n\geq 0\). This proves that there is a cluster of order \(4\) and size \(n\) for all \(n\geq 22\) and \(n=14,17,19,20\). To prove that there are no clusters of the remaining sizes we can simply do a computer search of all partitions of the remaining integers. This proves (i).
For (ii), we find \(9\) periodic clusters of period \(9\), order \(8\) and size various \(n\), one for each congruence modulo \(9\).
\(\seteqnumber{0}{3.}{0}\)\begin{align*} \text {Size $180$:}& \\&(28,21,20,19,17,13,12^2,11^2,4^3,3,1),\quad (26,25,18,17,16^2,15,11,9^2,8,2^4,1^2), \\ &(25,23,19,18^2,17,16,9,8^2,6,2^6,1),\quad (23,22^2,21,17,15,14,13,6^2,5^2,4,1^7). \\ \text {Size $190$:} \\ &(29,23,20^2,18,15,13^2,11^2,5,4,3^2,1^2),\quad (28,25,19^2,17^2,15,12,10^2,7,3,2^3,1^2), \\ &(26,24,21,19^2,17^2,11,8^2,6,3,2^4,1^3),\quad (25,23^2,21,18,16^2,13,7^2,5^2,3,2,1^6). \\ \text {Size 128:} \\ & (20,17^2,11,9^3,8^3,5^2,2),\quad (19^2,16,10^2,9^3,7^3,4,1^2), \\ & (17,15^3,14^2,8,5^3,3^3,2^3),\quad (16^2,15^3,13,7^2,4^3,3^3,1^3). \\ \text {Size 192:} \\&(30,21^3,19,13^2,12^3,4^4,2),\quad (27^2,18^3,17^2,11,9^3,2^5,1^2), \\&(27,25,19^2,18^3,9^3,7,2^7),\quad (24^2,23^2,17,15^3,6^3,5^2,1^8). \\ \text {Size 130:} \\ &(19,17,16^2,10,8^2,7^3,5,4^2,2),\quad (18^2,17,15,9^2,8^2,6^3,5,3,1^2), \\ &(18,16^2,15^2,9,7,6^3,4^2,3^2,2),\quad (17^2,16^2,14,8^2,7,5^3,4^2,2,1^2). \\ \text {Size 140:} \\ &(21,17^3,12,9,8^4,4^3,3),\quad (20,17,16^3,11,7^4,4,3^4), \\ &(19^3,15,10^3,9,6^4,2,1^3),\quad (18^3,17,14,9^3,5^4,4,1^4). \\ \text {Size 159:} \\ &(25,19^2,16,14,11^2,10^3,4^3,2),\quad (23^2,17,14^2,13^2,10,8^3,2^3,1^2), \\&(22,20,17^2,16^2,13,7^3,5,2^6),\quad (20^2,19^2,16,14,11^2,5^3,4^2,1^6). \\ \text {Size 214:} \\ &(33,23^3,22,15,14^2,13^2,5,4^3,3,1),\quad (30,29,20^4,19,12,10^2,9,3,2^5,1^2), \\ &(30,28,21,20^4,11,10^2,8,3,2^6,1),\quad (27,26^2,25,18,17^3,7^2,6^2,5,2,1^8). \\ \text {Size 170:} \\ &(25,21,20,18,16,13,11^2,9^2,5,4,3^2,1^2),\quad (24,22,21,17,15,13^2,11,8^2,6,5,2^2,1^3), \\ &(24,21,19^2,17,15,11,10,8^2,5,3^3,2,1^2),\quad (23,21^2,19,16,14,12,11,7^2,5^2,3,2,1^4). \end{align*}
Since this covers all nine congruence classes, we prove the result. Using the symmetric Magma package, all clusters of size \(n\) have been constructed for \(n\leq 84\), and they all have order at most \(4\) apart from one for \(n=84\). □
There is an obvious question here, which is whether there are clusters of size \(8\) in the range \(85\leq n\leq 205\). The answer is ‘maybe’. First, by working with periodic clusters of order \(8\) and different periods, from \(7\) to \(10\), one is able to find clusters of order \(8\) and all sizes between \(182\) and \(205\), so one can reduce the bound to \(182\). (All such clusters appear in the periodic cluster database in the Magma package symmetric.)
The smallest cluster of order \(8\) has size \(84\) (it is of period \(7\)), and there are known (periodic) clusters of order \(8\) of all sizes from \(84\) to \(205\) apart from
\[ \{ 85, 86, 87, 88, 89, 90, 92, 93, 94, 95, 96, 97, 99, 100, 101, 102, 103, 104, 106, 107, 108, 109,\]
\[ 110,111, 114, 115, 116, 117, 118, 122, 125, 132, 135, 136, 138, 142, 143, 150, 151, 181 \}. \]
It is not known whether there are clusters of order \(8\) of these sizes, but it is certainly likely that there are clusters of some of the larger sizes in the list above. There is no cluster of order \(8\) and size up to \(83\) by an exhaustive computer search, but computer programs take inconveniently long times to prove this (the case \(n=82\) took around two weeks using a Magma program1) because keeping track of all of the multisets of hook lengths is challenging.
As an example we note that, of the 239 clusters of size \(70\) and order \(4\), only 89 come from a periodic cluster of size \(2\) (together with conjugate partitions). Accessing non-periodic clusters without an exhaustive search looks difficult.
Moving from the multisets having to coincide to coincidences of character degrees, we can prove much better bounds than those in Theorem 3.1. First, for \(n\leq 115\) we can use Magma to explicitly calculate \(m(n)\). It is given in Table 4.1. Combining this with Theorem 3.1 proves almost all of the next result.
1 This is why Table 4.1 stops at \(n=115\).
-
-
(i) We have that \(m(n)\geq 4\) if and only if \(n\geq 11\) or if \(n=6,7\).
-
(ii) We have that \(m(n)\geq 6\) if and only if \(n\geq 17\) or if \(n=13,14,15\).
-
(iii) We have that \(m(n)\geq 8\) if and only if \(n\geq 21\) or if \(n=17,19\).
In all cases, the same statement holds when restricting ones attention only to characters parametrized by partitions that are not self-conjugate. In particular, this means that for \(n\geq 17\), \(A_n\) possesses three irreducible characters of the same degree that extend to \(S_n\).
-
-
Proof. For the bound for \(m(n)\geq 4\), we can use Theorem 3.1 to prove the result for \(n\geq 22\), and then Table 4.1 for the remaining values of \(n\). For the second and third parts, Theorem 3.1 proves the result for \(n\geq 206\), and from the remark afterwards, we know the result for \(n\geq 182\). Table 4.1 gives us the result for \(n\leq 115\). At this point one can either check each value in the range \(116\leq n\leq 181\) individually that \(m(n)\geq 8\) just by calculating all character degrees one at a time until at least eight of the same are found, or use the other known clusters of order \(8\) to reduce the number of possible \(n\) for which a brute-force search is needed. Either way, this proves the result.
To prove the tighter statement about the partitions being not self-conjugate, periodic clusters automatically satisfy this statement, so we merely have to prove the result in the range \(2\leq n\leq 181\). In the symmetric package, the program MaximumMultiplicityOfSymmetricCharacterDegreeExceeds, which is fairly quick, has a parameter IgnoreSelfConjugatePartitions. Setting this to be true ignores irreducible characters parametrized by self-conjugate parameters, and can be used to verify the result in this range. □
From Table 4.1 we see what the answer should be for larger bounds: for \(m(n)\geq 10\) we need \(n\geq 25\), for \(m(n)\geq 12\) we need \(n\geq 28\), and so on. However, this is conjectural because we do not have a version of Theorem 3.1 for these values, to eliminate all but a small number of \(n\) that we can check individually. The proof in [3] gives no explicit bounds, and the version in [4] gives us bounds of the form \(m(n)\geq O(n^{1/7})\). These are obviously not useful for larger values of \(m(n)\).
One other option is, instead of considering the largest multiplicity \(m(n)\), to consider the average multiplicity. This is simply \(k(G)/|\cd (G)|\). For symmetric groups, \(k(S_n)\) is obviously the number of partitions of \(n\), so we are dividing the number of partitions of \(n\) by the number of irreducible character degrees of \(n\). If there were no coincidences of character degrees apart from conjugate partitions, the average multiplicity should be slightly below \(2\), because the number of self-conjugate partitions is small compared with the number of partitions.
However, we know that there are coincidences of character degrees, since \(m(n)\to \infty \) as \(n\to \infty \). Figure 3.1 gives the ratio \(k(S_n)/|\cd (S_n)|\) for \(1\leq n\leq 115\). It looks far from conclusive at this stage whether the average multiplicity has a limit (maybe 2.5?) or tends to infinity as \(n\) increases.2
We can ask the question for arbitrary finite groups, a significant strengthening of the result by Moretó [17] and the author [3] on \(|G|\) being bounded by a function of \(m(G)\). In [17, p.245], Moretó asks this question specifically for soluble groups rather than all groups, but it looks as though this might be true, at least for all groups other than symmetric groups.
2 In [17], Moretó calculated this ratio for \(n\leq 55\), but the general trend is not particularly obvious for those smaller values of \(n\).
The only reason that alternating groups are excluded from this is that Figure 3.1 does not compel the author to believe that the average multiplicity is unbounded for symmetric groups.
One could ask the dual question, and consider the multiset of conjugacy class sizes, and their multiplicities. This was considered in [10], where it was proved that the orders of finite soluble groups are bounded by a function of the maximal multiplicity of their conjugacy class sizes, and partially extended to all finite groups in [19]. In analogy with \(\cd (G)\), write \(\cc (G)\) for the set of conjugacy class sizes.
In other words, the average multiplicity of a conjugacy class size should tend to infinity as the group order does. The evidence for this for symmetric groups is much more convincing, and looks potentially easier to prove since centralizer sizes are easier to compute than character degrees. The graph, Figure 3.2, is a smooth exponential-like curve as well, suggesting an asymptotically accurate formula might even be findable.3
We note that Conjectures 3.3 and 3.4 hold for \(p\)-groups and soluble groups with trivial Frattini subgroup [18, Lemmas 2.2 and 2.3], and Lie-type groups of bounded rank by [17, Lemma 6.3]. Conjecture 3.3 is true for simple groups of Lie type by [13, Corollary 1.6].
Having discussed the first column of the character table, one could ask the question about more than one column. A question of Alexander Ryba was whether there are irreducible characters \(\lambda \) and \(\mu \) of \(S_n\) for \(n\geq 2\) such that \(\lambda (1)=\mu (1)\) and \(\lambda ((1,2))=\mu ((1,2))\neq 0\) (so that \(\lambda \) and \(\mu \) are not conjugate)? The first such case is for \(S_{12}\), where the characters associated to the partitions \((7,1,1,1,1,1)\) and \((4,4,4)\) have the same character degree and value on an involution. By \(S_{30}\) there are 70 pairs of such partitions, and by \(S_{40}\) there are 314. The first \(n\) for which there are two characters with the same value on \(1\), \((1,2)\) and \((1,2,3,4)\) is \(35\).
In the other direction, there are four characters of \(S_{32}\) that share the same non-zero values on \(1\) and \((1,2)\) (so that they are not partitions and their conjugates), leading to the following reasonable-sounding conjecture.
3 Although it looks like an exponential curve, it cannot of course be strictly exponential because \(k(S_n)\) is not even exponential in \(n\).
-
Conjecture 3.5. Let \(X\) be a finite set of permutations, and let \(k\geq 1\) be an integer. For all sufficiently large \(n\), there exist \(k\) distinct irreducible characters of \(S_n\) whose values on permutations \(g\in S_n\) coincide for all \(g\) of cycle type in \(X\).
3.2 General linear groups
If one considers generic degrees for unipotent characters of \(\GL _n(q)\) rather than symmetric groups, the conjugate partition does not yield a character of the same degree in general, as Lusztig’s \(a\)-function should differ between a partition and its conjugate. If \(n=15\) then the partition \((6,3,2,2,2)\) has the property that it and its conjugate have the same \(a\)-function, which takes value \(21\). This is the smallest such coincidence: there are two for \(n=16\), none for \(n=17,18,23\), and at least one for all larger numbers. At the moment there is no general theory for generic degree multiplicities, so one cannot say much about such partitions. We can at least prove that there are always a pair of partitions with the same generic degree for all \(n\geq 24\).
-
Proof. We can prove the result generically for \(n\geq 28\). The partition \(\lambda =(7^2,4,3^3,1)\) has conjugate \(\lambda '=(7,6^2,3,2^3)\). A direct check shows that \(a(\lambda )=a(\lambda ')=57\). We can add \(m\) to the first part and \(m\) parts of size \(1\) to \(\lambda \) to make the partition \(\lambda ^{(m)}\). We have that
\[a(\lambda ^{(m)})=57+(7+8+\cdots +(m+6)),\]
and this is clearly the same for the conjugate partition. Thus there is a partition of \(28+2m\) with the desired property for all \(m\geq 0\).
Moreover, there is an addable node to \(\lambda \) in the \((4,4)\) position. This gives the partition \(\mu =(7^2,4^2,3^2,1)\), with conjugate \(\mu '=(7,6^2,4,2^3)\). As the box lies in the diagonal, \(a(\mu )=a(\mu ')=60\). We can form the partition \(\mu ^{(m)}\) in analogy with \(\lambda ^{(m)}\) by adding a box in the \((4,4)\) position to \(\lambda ^{(m)}\) (or by extending the first row and column of \(\mu \)) to obtain a partition with the desired property for all odd integers at least \(29\).
For integers less than \(28\), we simply list partitions with the desired property.
\[ (6,3,2^3), \quad (6,3^2,2^2),\quad (7,3^3,2,1),\quad (6,4^2,3^2),\quad (6,4^3,3),\quad (8,4,3,2^3,1),\]
\[ (8,4^2,3,2^2,1),\quad (8,4^3,2^2,1),\quad (9,4,3^3,2^2),\quad (8,5^2,3,2^3).\]
Proving that no other integer works requires checking all partitions for each individual \(n\), which uses a computer (or can be done by hand for very small \(n\)). □
On the other hand, using a database of all clusters of partitions of size at most 60, we find exactly three pairs of non-conjugate partitions whose unipotent generic degree is the same. The general methods and constructions from [3] give no control over the \(a\)-function, so this area is wide open. It seems ambitious to offer a conjecture on no evidence at all, so instead we should phrase it as a question.
It seems reasonable that the maximal multiplicity will, at some point, exceed \(2\), although it does not for \(n\leq 84\). (We can check this because all clusters of size at most \(84\) are known, and in the symmetric package database.) It is not so clear at this stage whether the generic degree multiplicities should tend to infinity, or even be unbounded.
4 Largest degrees for symmetric groups
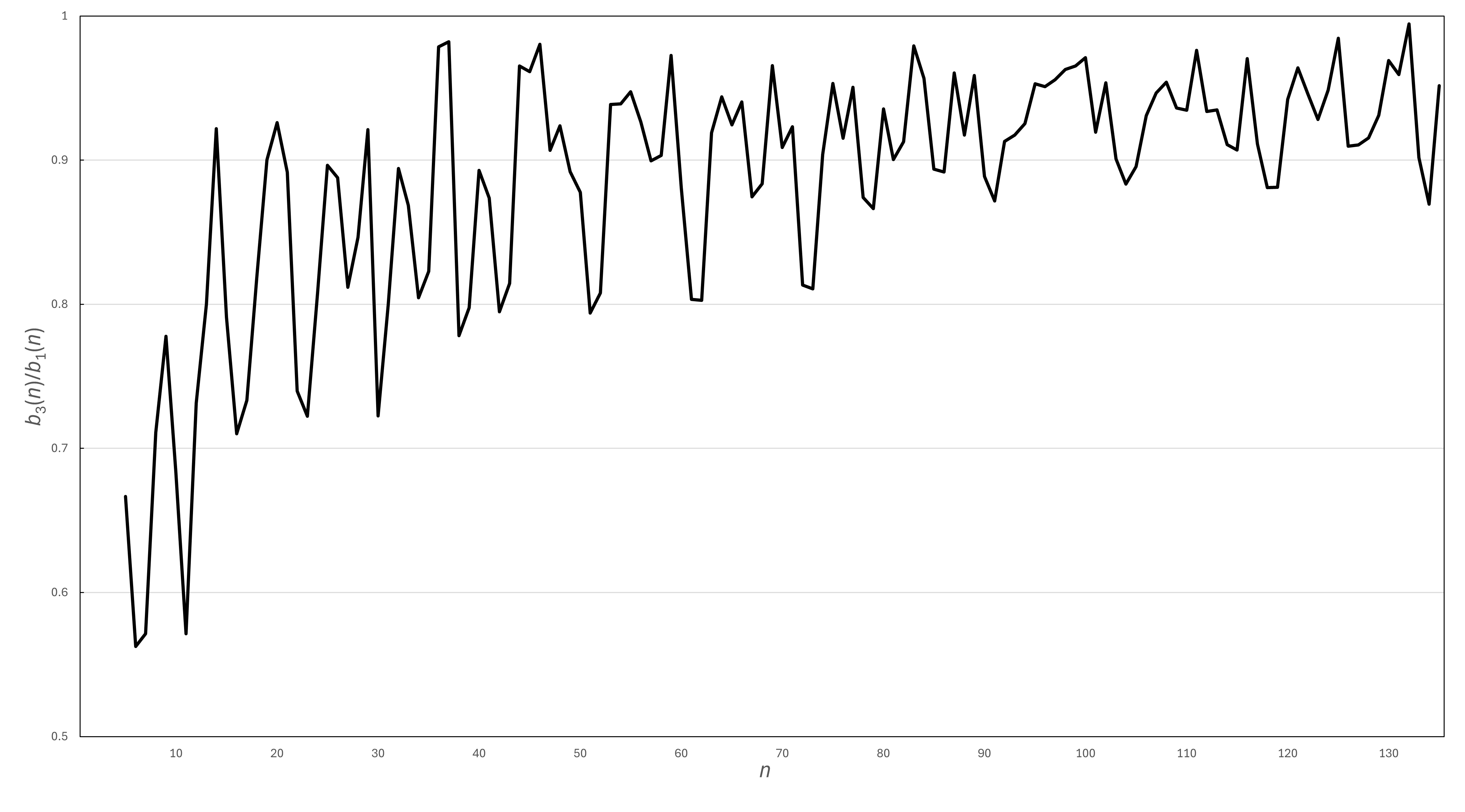
We now look at the largest degrees of symmetric groups. The first article about this was by McKay [16], who computed \(b_1(n)\) for \(n\leq 75\). In the symmetric package we list the values for \(b_1(n)\), \(b_2(n)\) and \(b_3(n)\) for \(n\leq 135\), together with the partitions that reach these values. This allows us to consider the fraction \(b_i(n)/b_1(n)\) for \(i=2,3\).
As stated in the introduction, Halasi, Hannusch and Nguyen [8] proved that the sums of the squares of all irreducible character degrees other than the largest exceeds twice the square of the largest degree.
Figure 4.1 gives the ratio \(b_3(n)/b_1(n)\) for \(n\) up to \(135\), and from this it is easy to see that \(b_3(n)/b_1(n)\) and \(b_2(n)/b_1(n)\) are bounded below by \(0.8\) for all \(52\leq n\leq 135\), and highly likely that this is true for all larger \(n\). If \(b_3(n)\) and \(b_2(n)\) are each achieved by a unique (necessarily self-conjugate) character then the sum of the squares of character degrees that are \(b_2(n)\) or \(b_3(n)\) is less than \(2b_1(n)^2\), and otherwise it exceeds \(2b_1(n)^2\). (See Conjecture 4.1 below.)
Can both the second- and third-largest degrees be achieved by unique characters? Yes. The cases \(n=19,59\) are the only ones for which this occurs up to \(n=135\), but there is no reason to believe that it will not occur again. Thus we have the following conjecture, where we have to exclude some small \(n\).
-
Conjecture 4.1. Let \(n\) be an integer with \(n\geq 5\), \(n\neq 6,7\).
-
(i) If \(n\neq 11\), then \(b_1(n)^2\leq b_2(n)^2+b_3(n)^2\).
-
(ii) If \(n\neq 6,7,11,16,38\), and \(b_2(n)\) or \(b_3(n)\) is achieved by two or more irreducible characters of \(S_n\), then
\[ \sum _{\substack {\chi \in \Irr (S_n)\\\chi (1)\in \{b_2(n),b_3(n)\}}}\chi (1)^2>2b_1(n)^2.\]
-
(iii) If \(b_2(n)\) and \(b_3(n)\) are both achieved by a unique irreducible character of \(S_n\) then
\[ \sum _{\substack {\chi \in \Irr (S_n)\\\chi (1)\in \{b_2(n),b_3(n),b_4(n)\}}}\chi (1)^2>2b_1(n)^2.\]
-
(iv) If \(n\geq 62\) then \(2b_1(n)^2\leq b_2(n)^2+b_3(n)^2+b_4(n)^2\).
-
For the last part of this conjecture, in the region \(13 \leq n\leq 61\) the statement holds unless \(n\) lies in
\[ \{15,16,17,22,23,27,30,34,38,42,51,61\}.\]
This conjecture has been checked up to \(n=100\) (the value for \(b_4(n)\) is not in the symmetric package, and had to be computed separately), and should hold for large \(n\) as the ratios \(b_3(n)/b_1(n)\) and \(b_2(n)/b_1(n)\) approach \(1\), so the inequality almost holds even without the contribution of \(b_4(n)^2\).
There have been a number of papers in the last few decades about large-degree characters, and a continuous version of the hook formula. We specifically mention [22, Theorem 2]; this theorem states, loosely speaking, that the squares of the degrees of the ‘large-degree’ characters of \(S_n\) sum to \(n!-o(n!)\), i.e., most of the order of the group. On the other hand, [22, Theorem 1] bounds \(b_1(n)\) well away from \(\sqrt {n!}\), meaning that there must be unboundedly many large-degree characters of \(S_n\).
The main barrier to these two theorems implying the following conjecture is that we do not know whether there is only boundedly characters for each of these large degrees \(b_i(n)\).
Although there is a significant amount of noise in Figure 4.1, there is a clear trend. One can see this intuitively: the expectation is that, for large \(n\), partitions that are close to the LSVK curve (which was independently discovered by Logan and Shepp [14] and Vershik and Kerov [21]) should yield the largest-degree characters. For large \(n\), there are many partitions that are arbitrarily close to this curve, so for any fixed \(m\) there are \(m\) characters of degree all very close to the maximum.
Despite several papers being written on the subject (most recently, for example, [7]), we do not have an algorithm to give the largest degree, even conjecturally. Ideas like that the largest character degree should be parametrized by a partition \(\lambda \) that is ‘very close’ to a self-conjugate partition (as considered in [23, Section 3] and subsequent papers by this group of authors) appear perhaps to not hold in general, based on our evidence here. For example, if \(n=96,109,123\) then one must remove four boxes to arrive at a self-conjugate partition. (These are the only such \(n\) up to \(135\).) This is despite the fact that \(b_1(n)\) for \(n=94,107,121\) being realized by a self-conjugate partition; in general, one cannot find \(b_1(n)\) by adding a box to the partition realizing \(b_1(n-1)\) and choosing the partition with largest degree, i.e., inducing the largest-degree character from \(S_{n-1}\). The first \(n\) for which one needs to add three boxes to a self-conjugate partition to obtain a partition realizing \(b_1(n)\) is \(n=37\), and then one needs three boxes for \(n=45,54,83,95,97,102,108,110,122,124\) up to \(135\).
Indeed, one actually needs to subtract five boxes from the partition witnessing \(b_1(132)\) to obtain a self-conjugate partition. This leads the author to suspect that the answer to the following question is ‘no’.
The question, at first glance, should intuitively have a positive answer. The idea is supposed to be that as \(n\) increases one should be able to get arbitrarily close to the LSVK curve, which is self-conjugate, so you should not need to remove more than a couple of boxes to hit something self-conjugate. Unfortunately it does not look from the data as though things are tending towards being closer and closer to a self-conjugate partition, in fact the opposite, given the five boxes needed for \(n=132\).
This suggests that any form of ‘shaking algorithm’4 alluded to above (see, for example, [7]) is doomed to fail to determine \(b_1(n)\) efficiently in the long run.
| \(n\) | \(m(n)\) | \(n\) | \(m(n)\) | \(n\) | \(m(n)\) | \(n\) | \(m(n)\) |
| \(4\) | \(2\) | \(32\) | \(12\) | \(60\) | \(34\) | \(88\) | \(78\) |
| \(5\) | \(2\) | \(33\) | \(16\) | \(61\) | \(44\) | \(89\) | \(94\) |
| \(6\) | \(4\) | \(34\) | \(18\) | \(62\) | \(30\) | \(90\) | \(102\) |
| \(7\) | \(4\) | \(35\) | \(30\) | \(63\) | \(44\) | \(91\) | \(84\) |
| \(8\) | \(2\) | \(36\) | \(14\) | \(64\) | \(36\) | \(92\) | \(84\) |
| \(9\) | \(3\) | \(37\) | \(20\) | \(65\) | \(52\) | \(93\) | \(94\) |
| \(10\) | \(2\) | \(38\) | \(26\) | \(66\) | \(34\) | \(94\) | \(80\) |
| \(11\) | \(4\) | \(39\) | \(16\) | \(67\) | \(54\) | \(95\) | \(104\) |
| \(12\) | \(4\) | \(40\) | \(20\) | \(68\) | \(38\) | \(96\) | \(96\) |
| \(13\) | \(6\) | \(41\) | \(22\) | \(69\) | \(56\) | \(97\) | \(104\) |
| \(14\) | \(6\) | \(42\) | \(20\) | \(70\) | \(50\) | \(98\) | \(104\) |
| \(15\) | \(6\) | \(43\) | \(26\) | \(71\) | \(48\) | \(99\) | \(96\) |
| \(16\) | \(4\) | \(44\) | \(25\) | \(72\) | \(44\) | \(100\) | \(104\) |
| \(17\) | \(8\) | \(45\) | \(24\) | \(73\) | \(50\) | \(101\) | \(110\) |
| \(18\) | \(6\) | \(46\) | \(24\) | \(74\) | \(44\) | \(102\) | \(106\) |
| \(19\) | \(10\) | \(47\) | \(32\) | \(75\) | \(58\) | \(103\) | \(112\) |
| \(20\) | \(6\) | \(48\) | \(16\) | \(76\) | \(46\) | \(104\) | \(102\) |
| \(21\) | \(8\) | \(49\) | \(32\) | \(77\) | \(60\) | \(105\) | \(146\) |
| \(22\) | \(8\) | \(50\) | \(30\) | \(78\) | \(48\) | \(106\) | \(104\) |
| \(23\) | \(12\) | \(51\) | \(26\) | \(79\) | \(58\) | \(107\) | \(120\) |
| \(24\) | \(8\) | \(52\) | \(24\) | \(80\) | \(64\) | \(108\) | \(114\) |
| \(25\) | \(12\) | \(53\) | \(32\) | \(81\) | \(72\) | \(109\) | \(132\) |
| \(26\) | \(12\) | \(54\) | \(32\) | \(82\) | \(56\) | \(110\) | \(126\) |
| \(27\) | \(10\) | \(55\) | \(40\) | \(83\) | \(58\) | \(111\) | \(136\) |
| \(28\) | \(12\) | \(56\) | \(32\) | \(84\) | \(66\) | \(112\) | \(126\) |
| \(29\) | \(22\) | \(57\) | \(34\) | \(85\) | \(86\) | \(113\) | \(130\) |
| \(30\) | \(14\) | \(58\) | \(32\) | \(86\) | \(68\) | \(114\) | \(108\) |
| \(31\) | \(12\) | \(59\) | \(32\) | \(87\) | \(86\) | \(115\) | \(144\) |
Table 4.1: The function \(m(n)\) for \(4\leq n\leq 115\).
| \(n\) | Number of pairs | \(n\) | Number of pairs | \(n\) | Number of pairs |
| \(15\) | \(1\) | \(51\) | \(311\) | \(87\) | \(23895\) |
| \(16\) | \(2\) | \(52\) | \(412\) | \(88\) | \(32343\) |
| \(17\) | \(0\) | \(53\) | \(380\) | \(89\) | \(31065\) |
| \(18\) | \(0\) | \(54\) | \(373\) | \(90\) | \(31942\) |
| \(19\) | \(1\) | \(55\) | \(500\) | \(91\) | \(37794\) |
| \(20\) | \(1\) | \(56\) | \(711\) | \(92\) | \(45633\) |
| \(21\) | \(5\) | \(57\) | \(786\) | \(93\) | \(52072\) |
| \(22\) | \(1\) | \(58\) | \(605\) | \(94\) | \(46924\) |
| \(23\) | \(0\) | \(59\) | \(695\) | \(95\) | \(54602\) |
| \(24\) | \(7\) | \(60\) | \(1331\) | \(96\) | \(78606\) |
| \(25\) | \(8\) | \(61\) | \(1241\) | \(97\) | \(77538\) |
| \(26\) | \(1\) | \(62\) | \(831\) | \(98\) | \(69055\) |
| \(27\) | \(5\) | \(63\) | \(1477\) | \(99\) | \(90644\) |
| \(28\) | \(13\) | \(64\) | \(2106\) | \(100\) | \(114893\) |
| \(29\) | \(6\) | \(65\) | \(1970\) | \(101\) | \(113891\) |
| \(30\) | \(10\) | \(66\) | \(1900\) | \(102\) | \(113139\) |
| \(31\) | \(10\) | \(67\) | \(2221\) | \(103\) | \(132908\) |
| \(32\) | \(17\) | \(68\) | \(2947\) | \(104\) | \(164782\) |
| \(33\) | \(30\) | \(69\) | \(3470\) | \(105\) | \(187349\) |
| \(34\) | \(11\) | \(70\) | \(3096\) | \(106\) | \(171432\) |
| \(35\) | \(25\) | \(71\) | \(3422\) | \(107\) | \(189781\) |
| \(36\) | \(57\) | \(72\) | \(5340\) | \(108\) | \(263020\) |
| \(37\) | \(33\) | \(73\) | \(5478\) | \(109\) | \(267378\) |
| \(38\) | \(21\) | \(74\) | \(4219\) | \(110\) | \(248100\) |
| \(39\) | \(49\) | \(75\) | \(6409\) | \(111\) | \(309322\) |
| \(40\) | \(93\) | \(76\) | \(8350\) | \(112\) | \(385150\) |
| \(41\) | \(64\) | \(77\) | \(7771\) | \(113\) | \(391224\) |
| \(42\) | \(60\) | \(78\) | \(8181\) | \(114\) | \(389427\) |
| \(43\) | \(93\) | \(79\) | \(9364\) | \(115\) | \(458881\) |
| \(44\) | \(108\) | \(80\) | \(12846\) | \(116\) | \(551870\) |
| \(45\) | \(172\) | \(81\) | \(14577\) | \(117\) | \(601380\) |
| \(46\) | \(111\) | \(82\) | \(11813\) | \(118\) | \(575444\) |
| \(47\) | \(102\) | \(83\) | \(14229\) | \(119\) | \(647147\) |
| \(48\) | \(293\) | \(84\) | \(21258\) | \(120\) | \(867144\) |
| \(49\) | \(284\) | \(85\) | \(21799\) | \(121\) | \(886962\) |
| \(50\) | \(172\) | \(86\) | \(18172\) | \(122\) | \(816004\) |
Table 4.2: Number of pairs of partitions \(\{\lambda ,\lambda '\}\) of size \(n\) with \(a(\lambda )=a(\lambda ')\), where \(\lambda '\) is the conjugate of \(\lambda \) (and \(\lambda \neq \lambda '\)).
4 Roughly speaking, a shaking algorithm involves finding a large-degree character of \(S_n\), restricting it to \(S_{n-k}\) for some fixed \(k\), then inducing the factors of this back up to \(S_n\) and looking for one with a larger degree. Combinatorially – using the branching rule – it involves finding all ways to remove \(k\) boxes, add \(k\) boxes back again, then determine the hook lengths of the resulting partition, hoping for something larger.
References
-
[1] Wieb Bosma, John Cannon, and Catherine Playoust, The Magma algebra system. I. The user language, J. Symbolic Comput. 24 (1997), 235–265.
-
[2] Roger Carter, Finite groups of Lie type, John Wiley & Sons, New York, 1985.
-
[3] David A. Craven, Symmetric group character degrees and hook numbers, Proc. Lond. Math. Soc. 96 (2008), 26–50.
-
[4] David A. Craven, Lower bounds for representation growth, J. Group Theory 13 (2010), 873–890.
-
[5] David A. Craven, Perverse equivalences and Broué’s conjecture II: The cyclic case, preprint, 2012.
-
[6] David A. Craven and Raphaël Rouquier, Perverse equivalences and Broué’s conjecture, Adv. Math. 248 (2013), 1–58.
-
[7] Vasilii Duzhin and Egor Smirnov-Maltsev, On Young diagrams of maximum dimension, Comm. Algebra 31 (2023), 33–47.
-
[8] Zoltán Halasi, Carolin Hannusch, and Hung Ngoc Nguyen, The largest character degrees of the symmetric and alternating groups, Proc. Amer. Math. Soc. 144 (2016), 1947–1960.
-
[9] Joan Herman and Fan Chung, Some results on hook lengths, Discrete Math. 20 (1977/78), 33–40.
-
[10] Andrei Jaikin-Zapirain, On two conditions on characters and conjugacy classes in finite soluble groups, J. Group Theory 8 (2005), 267–272.
-
[11] Gordon James, The representation theory of the symmetric groups, Lecture Notes in Mathematics, vol. 682, Springer-Verlag, Berlin, 1978.
-
[12] Gordon James and Adalbert Kerber, The representation theory of the symmetric group, Encyclopedia of Mathematics and its Applications, Addison-Wesley Publishing Co., Reading, MA, 1981.
-
[13] Martin Liebeck and Aner Shalev, Character degrees and random walks in finite groups of Lie type, Proc. London Math. Soc. 90 (2005), 61–86.
-
[14] Benjamin Logan and Lawrence Shepp, A variational problem for random Young tableaux, Adv. Math. 26 (1977), 206–222.
-
[15] Juan Martínez Madrid, The Baby Monster is the largest group with at most 2 irreducible characters with the same degree, Preprint, 1951.
-
[16] John McKay, The largest degrees of irreducible characters of the symmetric group, Math. Comp. 30 (1976), 624–631.
-
[17] Alexander Moretó, Complex group algebras of finite groups: Brauer’s problem 1, Adv. Math. 208 (2007), 236–248.
-
[18] Alexander Moretó, Multiplicities of character codegrees of finite groups, Bull. Lond. Math. Soc. 55 (2023), 234–241.
-
[19] Hung Ngoc Nguyen, Multiplicities of conjugacy class sizes of finite groups, J. Algebra 341 (2011), 250–255.
-
[20] Bruce Sagan, The symmetric group, second ed., Graduate Texts in Mathematics, vol. 203, Springer-Verlag, New York, 2001.
-
[21] Anatoly Vershik and Sergei Kerov, Asymptotics of the plancherel measure of the symmetric group and the limit form of Young tableaux, Soviet Math. Dokl. 18 (1977), 527–531.
-
[22] Anatoly Vershik and Sergei Kerov, Asymptotic behavior of the maximum and generic dimensions of irreducible representations of the symmetric group, Funktsional. Anal. i Prilozhen 19 (1985), 25–36 (Russian).
-
[23] Anatoly Vershik and Dmitry Pavlov, Numerical experiments in problems of asymptotic representation theory, J. Math. Sci. 168 (2010), 351–361.