Minesweeper and NP-completeness

My original paper appeared under this title in the Spring 2000 issue of the Mathematical Intelligencer (volume 22 number 2, pages 9--15).

It was discussed by Ian Stewart in the Mathematical Recreations column in the Scientific American, in October 2000, and has been discussed in newspapers in the USA (including the Boston Globe on November 1st, 2000) and on national radio in Britain. It has also featured on CNET (www.cnet.com) and CNN (www.cnn.com) and in the Guardian on 9th November, and there was an extensive discussion at slashdot (www.slashdot.com).

My work on Minesweeper was the subject of Ian Stewart's lecture at the Clay Institute on November 1st 2000.

I have just set up a FAQ list concerning minesweeper and NP-completeness which is available here. (But please read the current page first!)

What I managed to prove is that the minesweeper game is essentially equivalent in complexity to any of a wide range of known natural and important problems in the literature called NP-complete problems.

These problems all take the form of general problems requiring a yes/no answer. A rather nice example of such a problem is the "BIN-PACKING" problem (I prefer to call it "floppy-disk packing problem"!) which asks,

given n floppy disks each of size x and m computer files of sizes y₁, y₂, y₃, ... y_m, is it possible to copy all of the files to the floppy disks given?

Problems like this are of great practical importance, and an efficient algorithm would be very useful. Unfortunately no-one has yet found such an algorithm, and many people suspect that there isn't such an algorithm. In principle, it may even be possible to prove that there is no such algorithm, but again no-one has managed to do this either. Just about all that we do know is that if any one of the list of known NP-complete problems has an efficient algorithm, then they all do—and conversely if one of them can be proved not to have any efficient algorithm then they all have the same status.

The famous "P=NP?" question is just this: to determine whether there is an NP-complete problem which has an efficient algorithm (in which case they all would have), or alternatively to prove some NP-complete problem does not have an efficient algorithm (in which case none of them would have). This is one of the biggest and most important open problem in mathematics at the moment, and is the subject of a $1,000,000 prize offered by the Clay Mathematics Institute in the USA. See their site for some more details, in particular their pages on the P vs NP problem.

There are some very important reasons why one would want to know the answer to this question—whatever the answer would be. A "positive" answer giving new efficient algorithms would clearly be an important breakthrough, but even a "negative" answer that P is not equal to NP would have important practical consequences.

To understand why this is, you need to know that many codes used on computers and the internet are designed on the basis that a potential code-breaker would have to find an efficient algorithm for (at best) an NP-complete problem to break the code in reasonable time. These codes have proved to be remarkably effective. (In fact, because they are so good, they are—controversially—the subject of various laws against their use, put in place by national governments who seem to have accepted that they cannot break them. But that is another story.) However, the possibility that P and NP may turn out to be equal after all leaves a nagging doubt in the minds of the people who use these codes. This is because any person who can prove P=NP would be able to break them all. If he really wanted to make money, he might do a lot better than claiming the Clay Institute's million dollars!

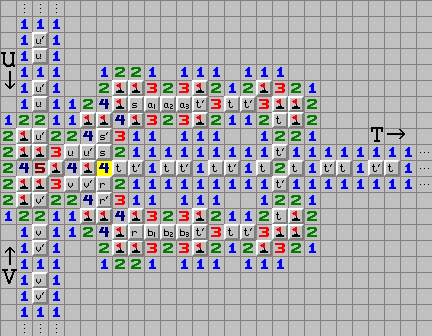
My result in the Mathematical Intelligencer states that a decision problem which I like to call "the Minesweeper Consistency Problem" and which is exactly equivalent to the problem of playing the minesweeper game, is yet another one of these NP-complete problems.

It's not entirely obvious how to convert the sorts of problems you get when playing the game to a simple decision problem with yes/no answers. However, a good Minesweeper player will never make a guess if there is a square that is certainly free and a guess is not required. Similarly he or she will mark up every mine that can be identified with certainty. It is precisely these questions, whether a mine is certainly in a particular square, or whether a square is certainly free, that can be solved by an algorithm for the Minesweeper Consistency Problem. See my Intelligencer paper for more details.

For the current discussion, it suffices that the problem of simply detecting which squares are or are not mines is equivalent to the Minesweeper Consistency Problem, and the fact that it is NP-complete means, for Minesweeper fans, that their favourite game can be seen as being right at the cutting edge of mathematical research. There are two possible viewpoints one might take on this.

The more "sober" viewpoint is that the NP-completeness of Minesweeper shows that Minesweeper really is a rather good game. The fact that it is NP-complete means that it is very difficult to spot when it is possible to clear a square safely in full knowledge that that square is clear, and when some guessing is required. In fact, even if you are told in advance that guessing is not required, it may still be difficult to decide what squares to clear. In some sense, when you play the game you cannot be expected to do much better than the hundreds of very good mathematicians who have worked on the P=NP? question for many many years.

But once again, there remains that nagging doubt... The more exciting view one might take is that one day, perhaps, it may turn out that an expert Minesweeper player could spot some pattern in the game that would eventually lead to an polynomial-time algorithm for solving it—and hence polynomial-time algorithms for all the NP-complete problems. Such an outcome would result in methods to crack all of the codes used in the internet and computers across the world.

I have written and maintain a companion world-wide-web paper, `Minesweeper configurations', which aims to contain some minesweeper configurations puzzles and problems that have come to light since the original paper. This is available here in PDF format.

In particular, I have already had one email pointing out that there is a small error in the diagram for a "bent wire" in the published paper and a have had email discussions with various people about simplifying the diagrams for the logic gates. The paper above contains details of some of these corrections and simplifications, and will be expanded in the future as more ideas and interesting positions come to light. Please email me with your ideas!

As mentioned above, there are algorithms that solve Minesweeper perfectly, but the only ones known take an inordinate amount of time. (Basically, this is because the game is played on a finite grid, so there are only finitely many possibilities to go through.) For a different slant on Minesweeper, you can also consider Minesweeper-like games on an infinite grid. This is what I did in a recent paper: I showed that in fact any computer program at all can be simulated by a position in such a game. See here for more details.

A minesweeper talk, first given at the ASE meeting in Birmingham, Jan 3-5 2003, is available (PDF file, 300k). This talk contains some nice graphics, and some new minesweeper configurations.

Note: "Minesweeper' here refers to the game of that name which is provided with Microsoft's "Windows" operating system. (I do not have any connection with Microsoft and nothing here should be regarded as comment on any of Microsoft's products.)

The diagrams in these pages are Minesweeper configurations that were used in the proof that the Minesweeper Consistency Problem is NP-complete. See the Intelligencer paper for more details. I am grateful to Harry Hutchinson for converting them to a more familiar format than the numbers and stars that I originally used.

Richard Kaye's main minesweeper page    Minesweeper and the P=NP? question FAQ    Richard Kaye's home page