Abstraction: proofs

Almost all students entering university and doing mathematics find the idea of proof difficult. This includes even many of the best students doing single honours maths. Gowers makes a tricky subject at least accessible. This topic is not easy, and it may even be the hardest chapter of the book, but you should get a good idea of what things are all about from this.

The example of lines cutting a circular disc into areas is beautiful. Most non-mathematicians would be perfectly convinced by the argument on page 35 and the top two lines of page 36. The fact that this convincing argument convinces you of something that is wrong makes the point very well: mathematics needs proof.

Another way of thinking about it concerns scale. Physics deals with objects astronomically large (the universe is perhaps ${10}^{27}$ metres in diameter) to miscroscopically tiny (an atom's nucleus is perhaps ${10}^{-14}$ metres in diameter) but maths deals with ${10}^{-10000000}$ to ${10}^{10000000}$ and much much more. Is it surprising our intuition (based on things of a human size) fails us for these very big or very small numbers?

Personally speaking, I very much like Gowers' presentation of proofs in practice as "abbreviated arguments" that any mathematician can and should be able to ask for clarification on points of detail or steps. This is how it works in practice and is a very good theoretical presentation of the ideas that are at work when we prove things.

Mathematical logic does, however, provide an alternative view: proofs in principle where this is a list of statements in a formal language where every step is permitted by a precise formal set of rules. The latter style of proof has the advantage that a computer can check correctness without requiring any intelligence, but the latter style of proof is impossible for humans to write. (Computer scientists have, for quite a number of years, been trying to develop systems where computers can write such proofs, usually aided by a human.)

Combining these two views gives us the best of both worlds. In a dispute between two mathematicians, one can ask the other for further verification of detailed points, but we know that the proof if correct can be written in a precise computer-checkable format, for which there will be no further argument should this level be reached: the computer is a perfect arbitrator. In practice, computers are rarely needed in this way, but much work has been done on computer proofs, and many people are interested in using computers a proof checkers of proof assistants. This work has been going on for 30 or 40 years. Perhaps in another 30 or 40 years computers will be really good at proofs.

All this is possible because proofs are structured in a pleasant way: proofs naturally break up into parts, and "subproofs" can be given for parts that were previously thought "obvious".

Of course, proofs rely on assumptions (axioms) and also rules of logic. As we discussed before, the number of axioms used in mathematics is huge, and Gowers gives at most a tiny sample. Rules of logic can also be given, and it turns out there is no real problem with these either. We have known precise rules of logic good enough for all mathematics for a bit over a hundred years.

You go home after your first term at university and join in the festivities at Christmas. Somehow or other you end up playing with your young cousin with her brand new Brio train set—a present from Santa. Between the two of you, you build this layout.

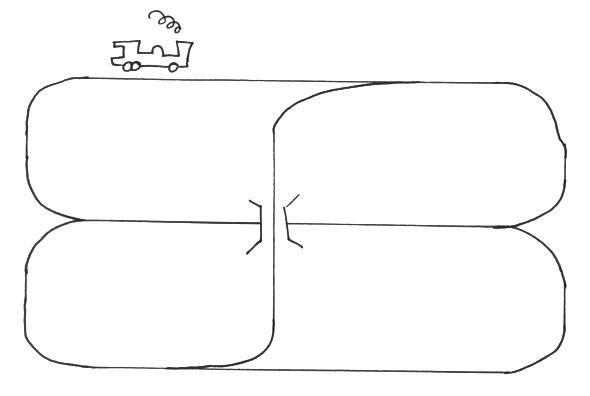
Your cousin puts a train on the track at the position indicated and wants to drive the train around the track without taking the wheels off the track to make it return to the same place, but turned round, i.e. pointing in the opposite direction. You can drive forwards or backwards, anywhere you like in the layout shown, and as far as you want. What is your answer?

Your uncle (the child’s father) overhears the conversation, and your answer. He has heard something about mathematics and how university math- ematicians are so keen at proving everything, and insists that you prove that your answer is correct to him. What do you say?

Your other cousin draws a layout on a piece of paper. It looks like this.

Before you start to try to make the layout you sit down and try to imagine a train somewhere on the track and you try and decide if it can turn round. What is your answer?

Since you are now rather familiar with the way Brio train sets work, you have a very good idea what pieces you need to build this second layout. The set you have got contains a bridge, the four junctions that are needed, and enough straight pieces and curves. Your aunt asks if you have everything you need to build the new layout. What is your answer?

Since Gowers gives a proof of Pythagoras' theorem, I can't resist giving my favourite proof of the theorem.

Take a right angled triangle ABC of sides $a,b,c$ where angle ACB is a right angle. (The convention has it that vertex A is opposite the side $a$ and so on, so $c$ is the hypotenuse.) Now draw a line going through the vertex C parallel to the side AB of length $c$ and mark the points D, E on this line so that ADEB makes a rectangle (so that angles ADC and CEB are right angles).

Since BA and DE are parallel the triangles ABC, BCE and CAD are all similar. That is they have the same angles and the same shape, but of course are of different sizes. But that means we can work out the length of sides EC and DC by proportions. These are $a^2/c$ and $b^2/c$. But as ABDE is a rectangle this means that

Rearranging, we get $a^2+b^2=c^2$, which is Pythagoras' theorem.

Why is this my favourite proof of Pythagoras? Because, unlike most proofs this one can be adapted to triangles that are not right angled.

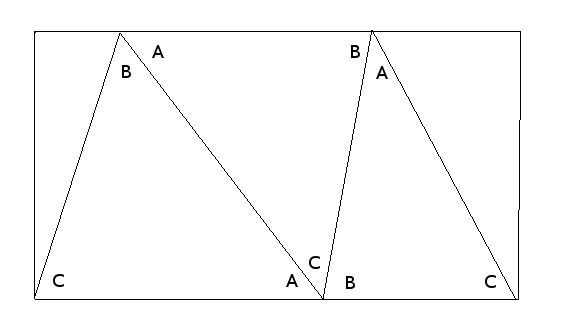
Take a triangle ABC of sides $a,b,c$. Draw a line DE parallel to BA so that triangles BCD, CAE and ABC are similar. (Here you need to pay attantion to the correspondence of vertices: the angle at B in triangle BCD should be the same as the angle at A in triangle ABC etc.) By proportions the lengths of the new sides are $ab/c$ for BD, $a^2/c$ for DC, $b^2/c$ for CE, and $ab/c$ for AE. Now drop perpendiculars from D and E to the line AB (which can be extended if necessary), so that the pirpendicular through D meets AB at D' and the pirpendicular through E meets AB at E'. So DEE'D' is a rectangle. By trigonometry, the small extra lengths D'B and E'A both have length $ab/c\cos C$ where $C$ is the angle at C in ABC. ($\cos C$ is negative if $C$ is more than ninety degrees, that's what we want.) Therefore equating the length of DE and D'E' we have

which rearranges to

This is called the cosine rule, and tells you how much Pythagoras's theorem has to be modified for a triangle which is not right-angled.

It is perhaps interesting how an argument for one theorem can sometime be modified to give an argument for a much stronger theorem. This is not always the case, of course!

Title: In what ways might one proof be better than another?

Give examples.

Conclusions: the idea of a "better" proof is unlikely to be particularly precise, but it is surprising how many mathematicians have opinions on this and how strong these opinions are!